
AllQuestion and Answers: Page 1391
Question Number 74162 Answers: 0 Comments: 0

Question Number 74161 Answers: 0 Comments: 0

Question Number 74160 Answers: 0 Comments: 0

Question Number 74168 Answers: 3 Comments: 1

Question Number 74155 Answers: 0 Comments: 0

Question Number 74148 Answers: 1 Comments: 0
Question Number 74144 Answers: 0 Comments: 0

Question Number 74143 Answers: 0 Comments: 0

Question Number 74142 Answers: 1 Comments: 0

Question Number 74141 Answers: 0 Comments: 1

Question Number 74140 Answers: 1 Comments: 0

Question Number 74139 Answers: 0 Comments: 1

Question Number 74138 Answers: 0 Comments: 2

Question Number 74137 Answers: 0 Comments: 2

Question Number 74131 Answers: 0 Comments: 2
Question Number 74130 Answers: 1 Comments: 0
Question Number 74129 Answers: 1 Comments: 0
Question Number 74123 Answers: 1 Comments: 2

Question Number 74121 Answers: 0 Comments: 1
Question Number 74117 Answers: 0 Comments: 1
Question Number 74112 Answers: 1 Comments: 0

Question Number 74111 Answers: 1 Comments: 1
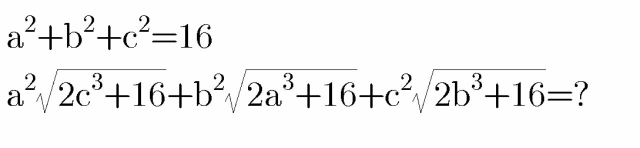
Question Number 74109 Answers: 1 Comments: 3

Question Number 74087 Answers: 0 Comments: 15
Question Number 74075 Answers: 0 Comments: 1
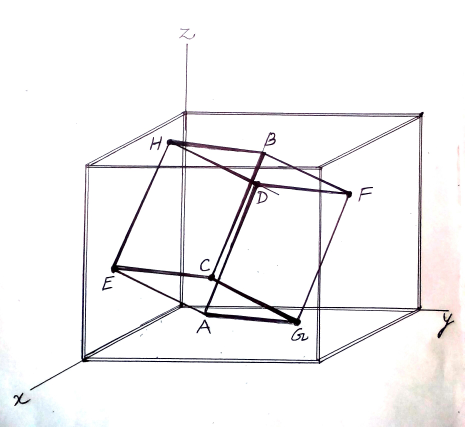
Question Number 74068 Answers: 1 Comments: 4

Pg 1386 Pg 1387 Pg 1388 Pg 1389 Pg 1390 Pg 1391 Pg 1392 Pg 1393 Pg 1394 Pg 1395
