
AllQuestion and Answers: Page 1388
Question Number 74821 Answers: 1 Comments: 0
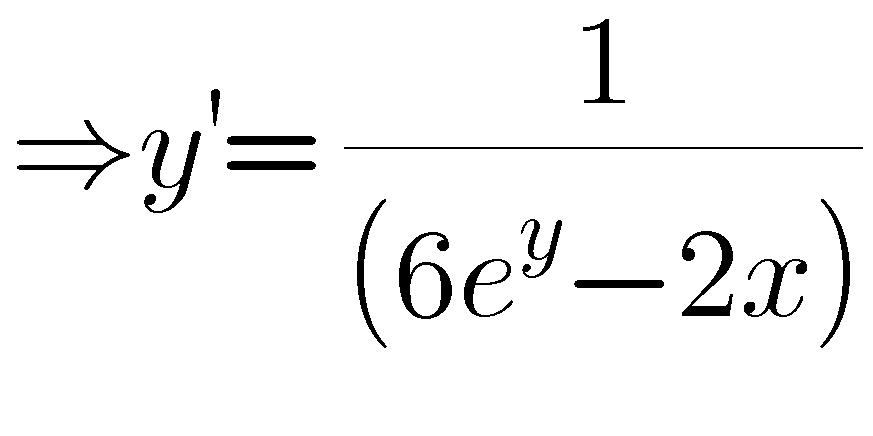
Question Number 74819 Answers: 1 Comments: 2
Question Number 74817 Answers: 1 Comments: 0

Question Number 74802 Answers: 1 Comments: 4

Question Number 74801 Answers: 2 Comments: 2
Question Number 74800 Answers: 1 Comments: 0
Question Number 74799 Answers: 1 Comments: 0
Question Number 74798 Answers: 0 Comments: 0
Question Number 74797 Answers: 0 Comments: 0
$${find}\:{nsture}\:{of}\:{the}\:{serie}\:\Sigma\:{sin}\left(\pi{en}!\right) \\ $$
Question Number 74796 Answers: 0 Comments: 0
Question Number 74795 Answers: 1 Comments: 1
Question Number 74794 Answers: 0 Comments: 2
Question Number 74790 Answers: 0 Comments: 0
Question Number 74786 Answers: 2 Comments: 1

Question Number 74793 Answers: 1 Comments: 1
Question Number 74782 Answers: 1 Comments: 2
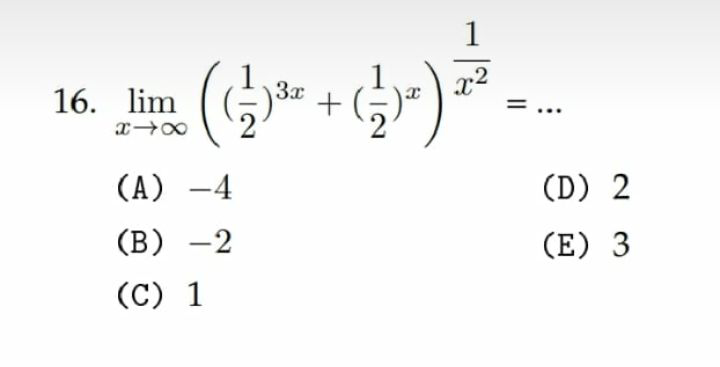
Question Number 74776 Answers: 1 Comments: 0
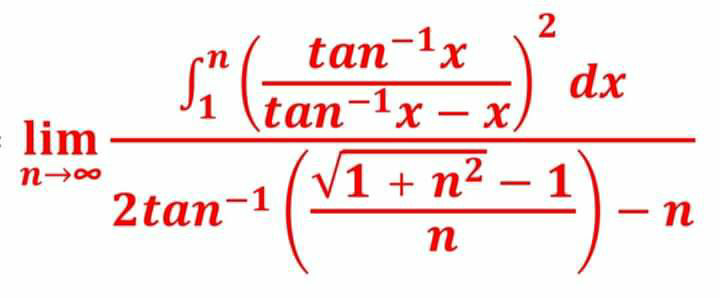
Question Number 74774 Answers: 0 Comments: 0

Question Number 74766 Answers: 0 Comments: 2

Question Number 74753 Answers: 1 Comments: 4
Question Number 74748 Answers: 1 Comments: 3

Question Number 74747 Answers: 1 Comments: 0
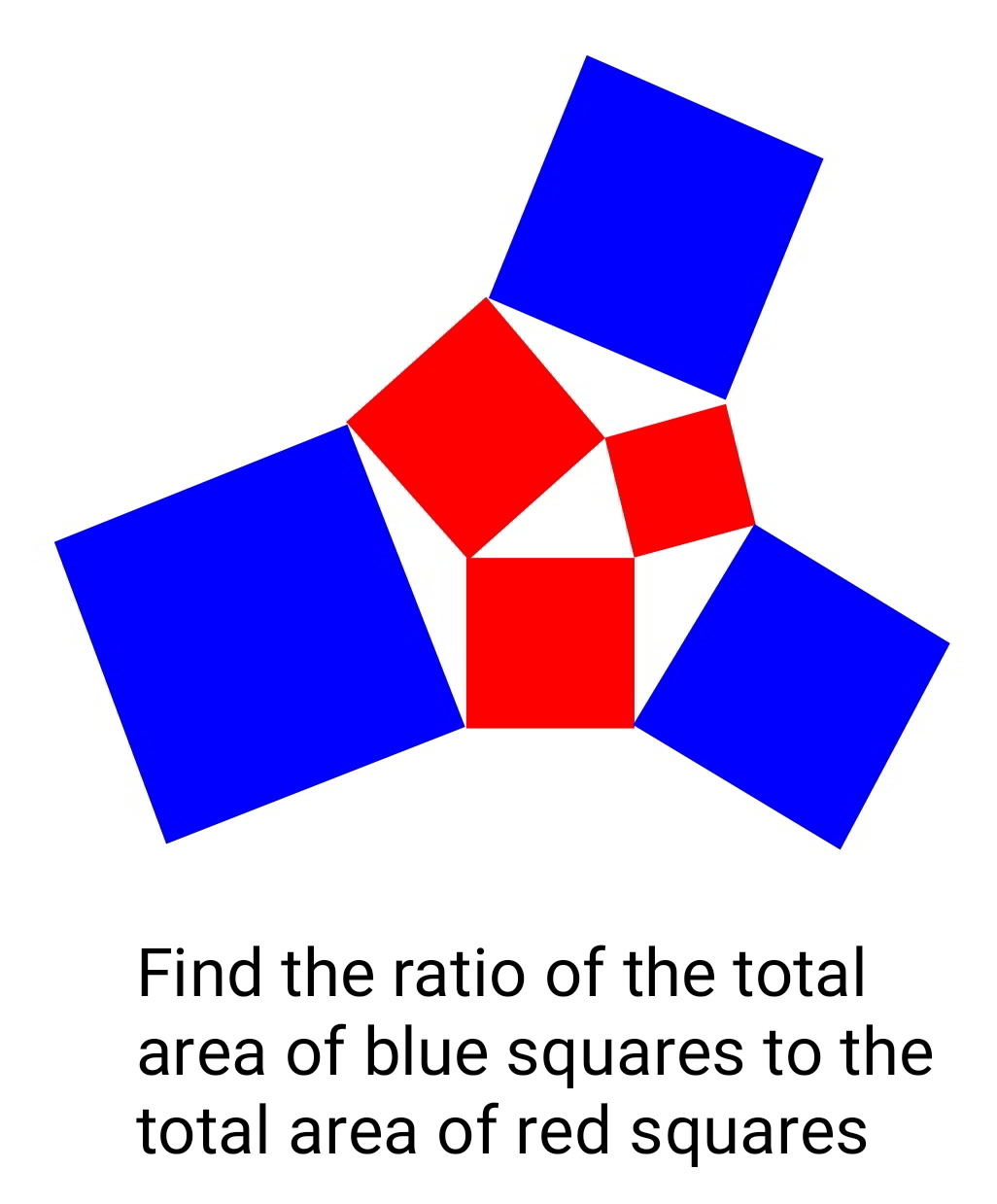
Question Number 74742 Answers: 2 Comments: 1
Question Number 74723 Answers: 1 Comments: 1
Question Number 74720 Answers: 2 Comments: 5

Question Number 74716 Answers: 1 Comments: 0

Pg 1383 Pg 1384 Pg 1385 Pg 1386 Pg 1387 Pg 1388 Pg 1389 Pg 1390 Pg 1391 Pg 1392
