
AllQuestion and Answers: Page 1386
Question Number 74620 Answers: 1 Comments: 0
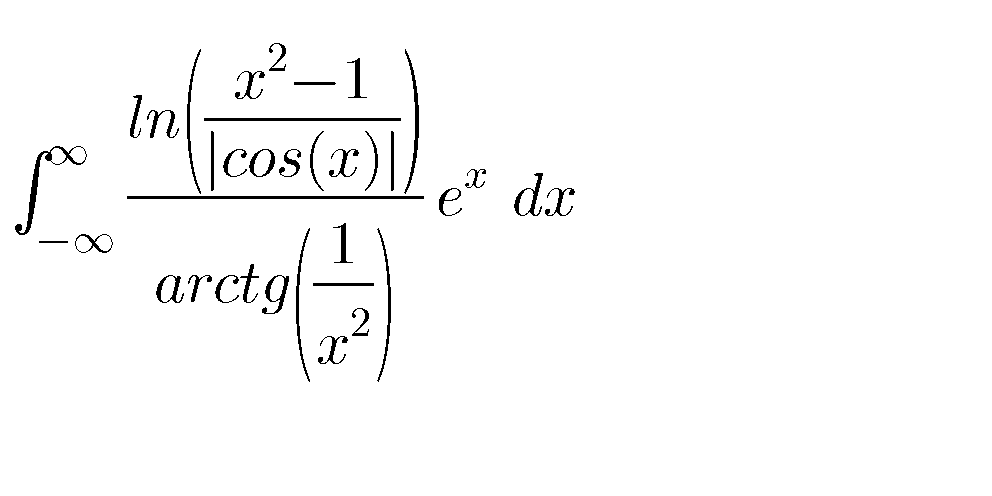
Question Number 74594 Answers: 1 Comments: 1

Question Number 74591 Answers: 0 Comments: 0

Question Number 74590 Answers: 1 Comments: 0

Question Number 74589 Answers: 1 Comments: 0

Question Number 74582 Answers: 1 Comments: 0
Question Number 74580 Answers: 1 Comments: 0
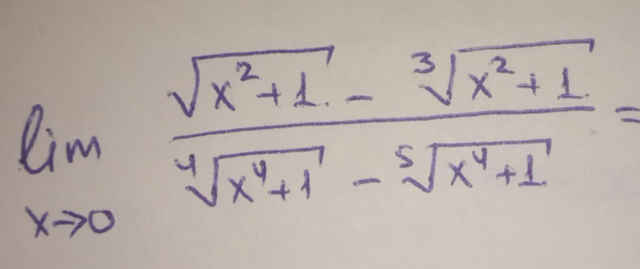
Question Number 74579 Answers: 0 Comments: 0
Question Number 74573 Answers: 1 Comments: 1
Question Number 74604 Answers: 0 Comments: 3
Question Number 74601 Answers: 0 Comments: 0
Question Number 74600 Answers: 1 Comments: 0

Question Number 74599 Answers: 0 Comments: 0
Question Number 74570 Answers: 1 Comments: 0
Question Number 74617 Answers: 0 Comments: 0
Question Number 74615 Answers: 2 Comments: 0

Question Number 74614 Answers: 1 Comments: 0

Question Number 74611 Answers: 1 Comments: 0
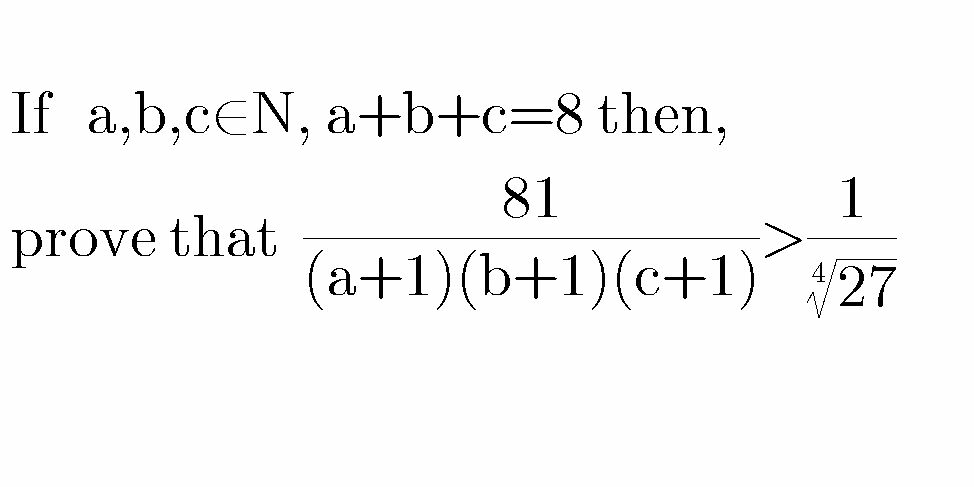
Question Number 74609 Answers: 0 Comments: 1
Question Number 74559 Answers: 0 Comments: 0
Question Number 74557 Answers: 1 Comments: 2

Question Number 74555 Answers: 0 Comments: 1
Question Number 74554 Answers: 1 Comments: 0
Question Number 74542 Answers: 1 Comments: 0
Question Number 74536 Answers: 1 Comments: 0
Question Number 74527 Answers: 2 Comments: 1
Pg 1381 Pg 1382 Pg 1383 Pg 1384 Pg 1385 Pg 1386 Pg 1387 Pg 1388 Pg 1389 Pg 1390
