Question and Answers Forum

AllQuestion and Answers: Page 1385

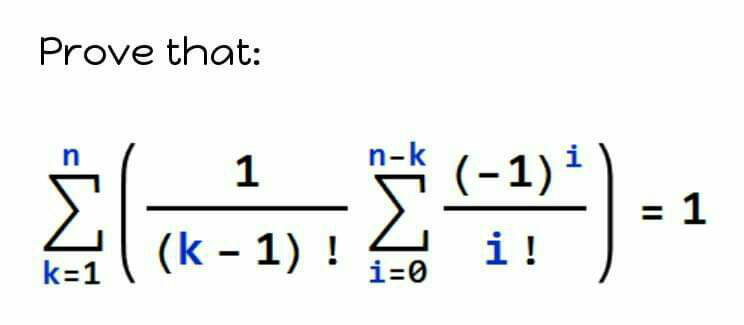
Question Number 73774 Answers: 0 Comments: 0

hello ,show that Σ_(n≥1) (((−1)^n nsin(n))/(1+n^2 ))=((πe^1 −πe^(−1) )/(−2e^π +2e^(−π) )) indication ,Residus Theorem let f(z)=((zsin(z))/((1+z^2 )sin(πz))) have a very nice day!

$$\mathrm{hello}\:,\mathrm{show}\:\mathrm{that} \\ $$$$\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{nsin}\left(\mathrm{n}\right)}{\mathrm{1}+\mathrm{n}^{\mathrm{2}} }=\frac{\pi\mathrm{e}^{\mathrm{1}} −\pi\mathrm{e}^{−\mathrm{1}} }{−\mathrm{2e}^{\pi} +\mathrm{2e}^{−\pi} } \\ $$$$\mathrm{indication}\:,\mathrm{Residus}\:\mathrm{Theorem}\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{zsin}\left(\mathrm{z}\right)}{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\mathrm{sin}\left(\pi\mathrm{z}\right)} \\ $$$$\mathrm{have}\:\mathrm{a}\:\mathrm{very}\:\mathrm{nice}\:\mathrm{day}! \\ $$

Question Number 73766 Answers: 3 Comments: 0

{ (((1/(x−1))=(2/(y−2))=(3/(z−3)))),((x+2y+3z=56)) :} please help me to solve it in R^3

$$\begin{cases}{\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{y}−\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{z}−\mathrm{3}}}\\{\mathrm{x}+\mathrm{2y}+\mathrm{3z}=\mathrm{56}}\end{cases} \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{in}\:\mathbb{R}^{\mathrm{3}} \\ $$

Question Number 73757 Answers: 1 Comments: 1

cos 70°+sin 200°=?

$$\mathrm{cos}\:\mathrm{70}°+\mathrm{sin}\:\mathrm{200}°=? \\ $$

Question Number 73755 Answers: 1 Comments: 0

show that for all integer n , n+1 divides (((2n)),(n) )

$${show}\:{that}\:\:\:{for}\:{all}\:{integer}\:\:{n}\:,\:\:{n}+\mathrm{1}\:{divides}\:\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix} \\ $$

Question Number 73751 Answers: 1 Comments: 1

Find out the value of J=∫_0 ^∞ ∫_0 ^1 (2e^(−2xy) −e^(−xy) )dxdy

$${Find}\:\:{out}\:{the}\:{value}\:{of}\:\:\: \\ $$$$\:\:{J}=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{e}^{−\mathrm{2}{xy}} −{e}^{−{xy}} \right){dxdy}\: \\ $$

Question Number 73746 Answers: 1 Comments: 1

total numper of words formed by 2 vowels and 3 consonants take from vowels and 5 consonants is equal to ? pleas sir help me ?

$${total}\:{numper}\:{of}\:{words}\:{formed}\:{by}\:\mathrm{2}\:{vowels}\:{and}\:\mathrm{3}\:{consonants}\:{take}\:{from}\:{vowels}\:{and}\:\mathrm{5}\:{consonants}\:{is}\:{equal}\:{to}\:? \\ $$$${pleas}\:{sir}\:{help}\:{me}\:? \\ $$

Question Number 73745 Answers: 0 Comments: 0

total numper of words formed by 2 vowels and 3 consonants take from vowels and 5 consonants is equal to ? pleas sir help me ?

Question Number 73744 Answers: 0 Comments: 0

total numper of words formed by 2 vowels and 3 consonants take from vowels and 5 consonants is equal to ? pleas sir help me ?

Question Number 73737 Answers: 2 Comments: 1

Question Number 73736 Answers: 1 Comments: 0

lim_(x→0) x^x

$$\underset{{x}\rightarrow\mathrm{0}} {{lim}x}^{{x}} \\ $$

Question Number 73730 Answers: 2 Comments: 0

Question Number 73725 Answers: 0 Comments: 0

Question Number 73724 Answers: 0 Comments: 0

find all simple graphical sequence for n=4

$${find}\:{all}\:{simple}\:{graphical}\:{sequence}\:{for}\:{n}=\mathrm{4} \\ $$

Question Number 73723 Answers: 0 Comments: 0

give two examples in support of understanding for enumerative combinatoris

$${give}\:{two}\:{examples}\:{in}\:{support}\:{of}\:{understanding}\:{for}\:{enumerative}\:{combinatoris} \\ $$

Question Number 73722 Answers: 0 Comments: 2

Question Number 73721 Answers: 0 Comments: 0

Question Number 73715 Answers: 1 Comments: 2

Evaluate the integral : ∫_( R) ∫(3x^2 +14xy+8y^2 )dxdy for the region R in the 1st quadrant bounded by the lines y=((−3)/2)x+1,y=((−3)/2)x+3,y=−(1/4)x and y=−(1/4)x+1 .

$${Evaluate}\:{the}\:{integral}\:: \\ $$$$\underset{\:\mathbb{R}} {\int}\int\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{14}{xy}+\mathrm{8}{y}^{\mathrm{2}} \right){dxdy}\:{for}\:{the}\:{region} \\ $$$$\mathbb{R}\:\mathrm{in}\:{the}\:\mathrm{1}{st}\:{quadrant}\:{bounded}\:{by}\:{the} \\ $$$${lines}\:{y}=\frac{−\mathrm{3}}{\mathrm{2}}{x}+\mathrm{1},{y}=\frac{−\mathrm{3}}{\mathrm{2}}{x}+\mathrm{3},{y}=−\frac{\mathrm{1}}{\mathrm{4}}{x} \\ $$$${and}\:{y}=−\frac{\mathrm{1}}{\mathrm{4}}{x}+\mathrm{1}\:. \\ $$

Question Number 73710 Answers: 0 Comments: 0