
AllQuestion and Answers: Page 1378
Question Number 75468 Answers: 0 Comments: 2
Question Number 75465 Answers: 0 Comments: 1
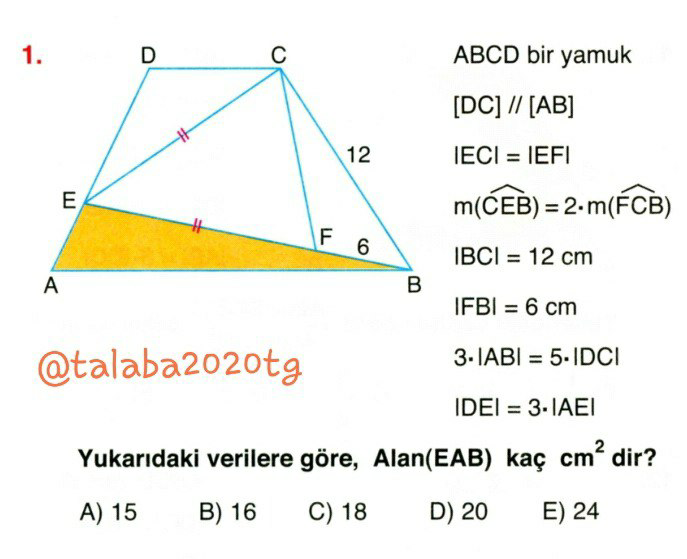
Question Number 75463 Answers: 2 Comments: 0

Question Number 75457 Answers: 2 Comments: 5
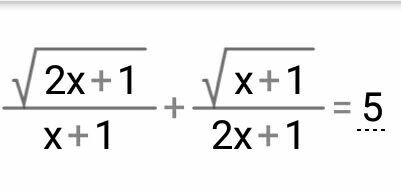
Question Number 75456 Answers: 2 Comments: 0
Question Number 75453 Answers: 0 Comments: 3

Question Number 75509 Answers: 1 Comments: 0
Question Number 75446 Answers: 1 Comments: 0
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}}{dx} \\ $$
Question Number 75445 Answers: 3 Comments: 0
Question Number 75444 Answers: 0 Comments: 1
Question Number 75440 Answers: 0 Comments: 3
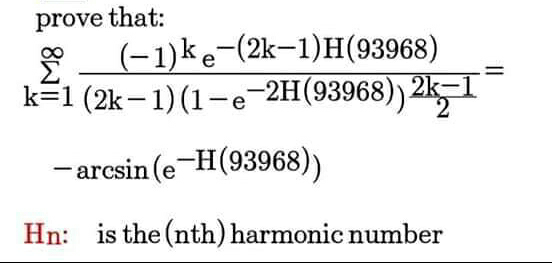
Question Number 75439 Answers: 1 Comments: 0
Question Number 75437 Answers: 1 Comments: 6
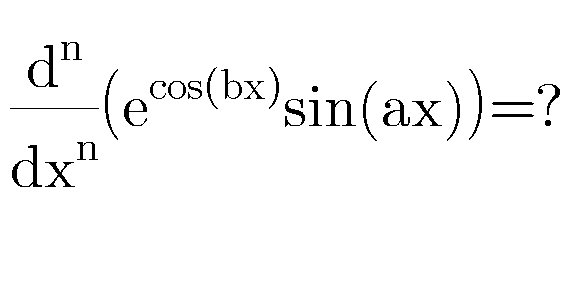
Question Number 75435 Answers: 0 Comments: 4
Question Number 75426 Answers: 1 Comments: 0
Question Number 75421 Answers: 0 Comments: 3
Question Number 75403 Answers: 1 Comments: 0

Question Number 75402 Answers: 0 Comments: 4
Question Number 75392 Answers: 1 Comments: 0
Question Number 75391 Answers: 0 Comments: 8

Question Number 75606 Answers: 1 Comments: 1

Question Number 75607 Answers: 0 Comments: 0
Question Number 75386 Answers: 1 Comments: 1

Question Number 75382 Answers: 1 Comments: 1
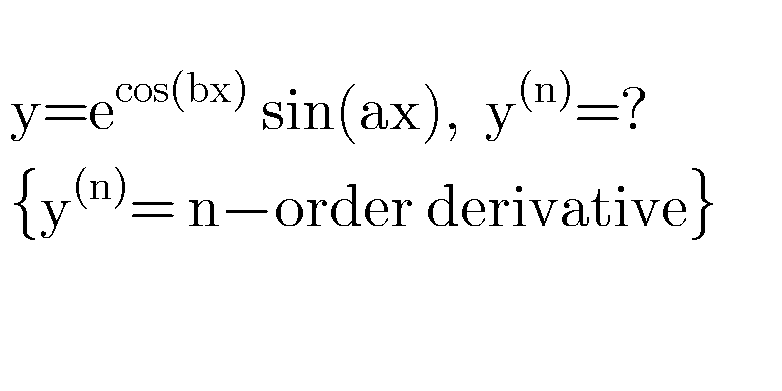
Question Number 75377 Answers: 0 Comments: 2

Question Number 75376 Answers: 1 Comments: 1

Pg 1373 Pg 1374 Pg 1375 Pg 1376 Pg 1377 Pg 1378 Pg 1379 Pg 1380 Pg 1381 Pg 1382
