
AllQuestion and Answers: Page 1373
Question Number 76428 Answers: 2 Comments: 0

Question Number 76424 Answers: 1 Comments: 1
Question Number 76407 Answers: 0 Comments: 0

Question Number 76404 Answers: 0 Comments: 2
Question Number 76401 Answers: 1 Comments: 0
Question Number 76397 Answers: 0 Comments: 2
Question Number 76386 Answers: 1 Comments: 2
Question Number 76384 Answers: 0 Comments: 1
Question Number 76368 Answers: 3 Comments: 5
Question Number 76367 Answers: 0 Comments: 4
Question Number 76361 Answers: 1 Comments: 3
Question Number 76360 Answers: 0 Comments: 1
Question Number 76359 Answers: 0 Comments: 1
Question Number 76356 Answers: 0 Comments: 1
Question Number 76355 Answers: 2 Comments: 0
$${find}\:\int\:\frac{{arctan}\left(\sqrt{\mathrm{1}+{x}}\right)}{\mathrm{2}+{x}}{dx} \\ $$
Question Number 76354 Answers: 0 Comments: 0
Question Number 76353 Answers: 0 Comments: 1
Question Number 76352 Answers: 0 Comments: 1
Question Number 76351 Answers: 0 Comments: 0
Question Number 76350 Answers: 0 Comments: 1
Question Number 76346 Answers: 1 Comments: 5

Question Number 76341 Answers: 0 Comments: 1

Question Number 76340 Answers: 3 Comments: 1

Question Number 76328 Answers: 0 Comments: 2

Question Number 76326 Answers: 2 Comments: 0
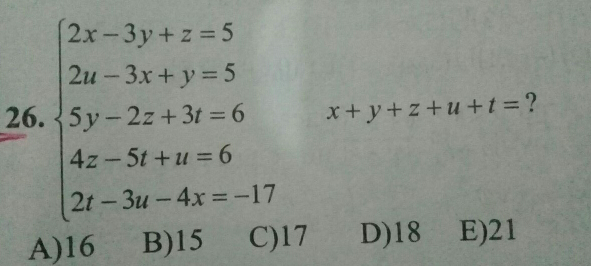
Question Number 76323 Answers: 0 Comments: 2

Pg 1368 Pg 1369 Pg 1370 Pg 1371 Pg 1372 Pg 1373 Pg 1374 Pg 1375 Pg 1376 Pg 1377
