
AllQuestion and Answers: Page 1372
Question Number 76088 Answers: 0 Comments: 2

Question Number 76087 Answers: 1 Comments: 0

Question Number 76086 Answers: 0 Comments: 0
Question Number 76075 Answers: 1 Comments: 0
Question Number 76061 Answers: 1 Comments: 0
Question Number 76053 Answers: 1 Comments: 2
$${how}\:{I}\:{calculate}\:\int\frac{\mathrm{1}}{{x}^{\mathrm{8}} +{x}^{\mathrm{2}} }{dx}\:? \\ $$
Question Number 76052 Answers: 0 Comments: 1

Question Number 76048 Answers: 2 Comments: 0
Question Number 76038 Answers: 1 Comments: 0

Question Number 76037 Answers: 1 Comments: 0
Question Number 76034 Answers: 1 Comments: 0
Question Number 76032 Answers: 0 Comments: 0

Question Number 76015 Answers: 0 Comments: 0

Question Number 76014 Answers: 0 Comments: 0

Question Number 76013 Answers: 1 Comments: 0

Question Number 76012 Answers: 1 Comments: 0
Question Number 76009 Answers: 1 Comments: 0
$${hiw}\:{do}\:{i}\:{solve} \\ $$$$\mathrm{2}^{{x}} \:=\:\mathrm{4}{x}? \\ $$
Question Number 76003 Answers: 1 Comments: 0
Question Number 75991 Answers: 1 Comments: 1

Question Number 75990 Answers: 0 Comments: 0

Question Number 75989 Answers: 0 Comments: 0

Question Number 75988 Answers: 0 Comments: 3

Question Number 75987 Answers: 1 Comments: 0

Question Number 75986 Answers: 1 Comments: 1
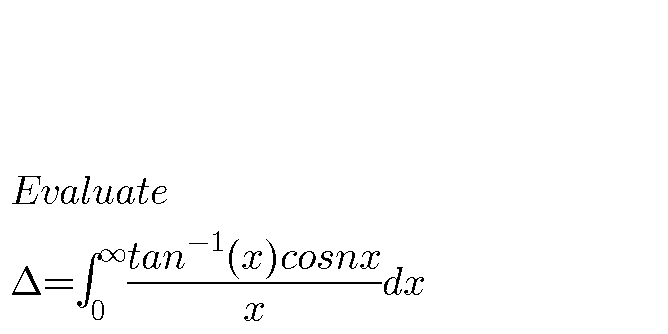
Question Number 75985 Answers: 1 Comments: 0

Question Number 75984 Answers: 1 Comments: 0

Pg 1367 Pg 1368 Pg 1369 Pg 1370 Pg 1371 Pg 1372 Pg 1373 Pg 1374 Pg 1375 Pg 1376
