Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1371

Question Number 68966 Answers: 0 Comments: 4

Question Number 68965 Answers: 0 Comments: 2

Question Number 68964 Answers: 0 Comments: 1

Question Number 68962 Answers: 0 Comments: 4

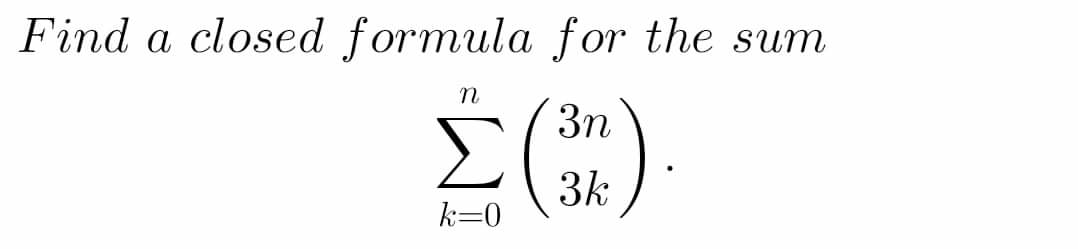
Question Number 68961 Answers: 1 Comments: 0

Question Number 68960 Answers: 0 Comments: 3

Question Number 68956 Answers: 0 Comments: 0

Question Number 68952 Answers: 1 Comments: 0

Question Number 68947 Answers: 0 Comments: 0

please utilise cette fonction to show that N∗N is denombrable f:N⊛N→N (x,y)∣→(((x+y)(x+y+1))/2)+y montrer que f est bijective Please help

$$\mathrm{please} \\ $$$$\mathrm{utilise}\:\mathrm{cette}\:\mathrm{fonction}\:\mathrm{to}\: \\ $$$$\mathrm{sh}\boldsymbol{\mathrm{ow}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{N}}\ast\boldsymbol{\mathrm{N}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{denombrable}} \\ $$$$\:\mathrm{f}:\boldsymbol{\mathrm{N}}\circledast\boldsymbol{\mathrm{N}}\rightarrow\boldsymbol{\mathrm{N}} \\ $$$$\:\:\:\:\left(\mathrm{x},\mathrm{y}\right)\shortmid\rightarrow\frac{\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{y} \\ $$$$\mathrm{montrer}\:\mathrm{que}\:\mathrm{f}\:\mathrm{est}\:\mathrm{bijective} \\ $$$$\:\:\:\boldsymbol{\mathrm{P}}\mathrm{lease}\:\mathrm{help} \\ $$$$ \\ $$$$\:\:\:\:\:\: \\ $$

Question Number 68946 Answers: 0 Comments: 1

Question Number 68941 Answers: 3 Comments: 3

Question Number 68935 Answers: 2 Comments: 0

Find all values for x: (x^2 −7x+11)^(x^2 −13x+42) =1 (Easy)

$${Find}\:{all}\:{values}\:{for}\:\boldsymbol{{x}}: \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{11}\right)^{{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{42}} =\mathrm{1} \\ $$$$\left({Easy}\right) \\ $$

Question Number 68930 Answers: 0 Comments: 3

In the figure we have 7 circles having the same radius. Determine the ratio between the perimeter of one of the circle and the perimeter of the gray region.

$$\mathrm{In}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{we}\:\mathrm{have}\:\mathrm{7}\:\mathrm{circles}\:\mathrm{having} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{radius}.\:\mathrm{Determine}\:\mathrm{the}\:\mathrm{ratio} \\ $$$$\mathrm{between}\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{of}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{circle}\:\mathrm{and}\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{of}\:\mathrm{the}\:\mathrm{gray}\:\mathrm{region}. \\ $$

Question Number 68926 Answers: 0 Comments: 0

Question Number 68925 Answers: 0 Comments: 2

Question Number 68924 Answers: 0 Comments: 0

Question Number 68923 Answers: 0 Comments: 2

Question Number 68912 Answers: 1 Comments: 0

Question Number 68899 Answers: 0 Comments: 9

solve for x and y the equation 2lnx −lny =ln(5x−6y)

$${solve}\:{for}\:{x}\:{and}\:{y}\:{the}\:{equation} \\ $$$$\:\mathrm{2}{lnx}\:−{lny}\:={ln}\left(\mathrm{5}{x}−\mathrm{6}{y}\right) \\ $$

Question Number 68898 Answers: 0 Comments: 7

solve for x the equation log_x e^(2x) = eln x −e

$${solve}\:{for}\:{x}\:{the}\:{equation} \\ $$$$\:\:{log}_{{x}} {e}^{\mathrm{2}{x}} \:=\:{eln}\:{x}\:−{e} \\ $$

Question Number 68885 Answers: 0 Comments: 2

if f(x)=((∣x∣)/x) g(x)=x^2 −1 find lim_(x→1) f(g(x))

$${if}\: \\ $$$${f}\left({x}\right)=\frac{\mid{x}\mid}{{x}} \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{1} \\ $$$$ \\ $$$${find}\: \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {{lim}}\:\:{f}\left({g}\left({x}\right)\right) \\ $$

Question Number 68879 Answers: 0 Comments: 2

let I =∫_0 ^1 (x/(ln(1+x)))dx determine a approximate value of I

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{{ln}\left(\mathrm{1}+{x}\right)}{dx}\:\:{determine}\:{a}\:{approximate}\:{value}\:{of}\:{I} \\ $$

Question Number 68878 Answers: 0 Comments: 0

find ∫((2(√x)+1)/(x^2 +1−(√(x^2 +1))))dx

$${find}\:\int\frac{\mathrm{2}\sqrt{{x}}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$

Question Number 68877 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) ((xdx)/((x^2 −x+i)^2 )) with i^2 =−1

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{xdx}}{\left({x}^{\mathrm{2}} −{x}+{i}\right)^{\mathrm{2}} }\:\:\:\:\:{with}\:{i}^{\mathrm{2}} =−\mathrm{1} \\ $$

Question Number 68876 Answers: 0 Comments: 2

calculate ∫_0 ^∞ (((−1)^x )/((3+x^2 )^2 ))dx

$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{x}} }{\left(\mathrm{3}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$

Question Number 68874 Answers: 0 Comments: 1

calculate ∫_0 ^(2π) (dx/(1+cosx +3sinx))

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dx}}{\mathrm{1}+{cosx}\:+\mathrm{3}{sinx}} \\ $$

Pg 1366 Pg 1367 Pg 1368 Pg 1369 Pg 1370 Pg 1371 Pg 1372 Pg 1373 Pg 1374 Pg 1375

Contact: info@tinkutara.com