Question and Answers Forum

AllQuestion and Answers: Page 1367

Question Number 77117 Answers: 0 Comments: 0

Interview indicates that all the 4 maths students,5 physics and 7 chemistry students who applied for a scholarship in their respective disciplines qualified for an award. In how many ways the aeard can be made if; (i)only one scholarship is available in each of the disciplines (ii)only two scholarships are availablr in each of the disciplines.

$${Interview}\:{indicates}\:{that}\:{all}\:{the}\:\mathrm{4}\:{maths} \\ $$$${students},\mathrm{5}\:{physics}\:{and}\:\mathrm{7}\:{chemistry} \\ $$$${students}\:{who}\:{applied}\:{for}\:{a}\:{scholarship} \\ $$$${in}\:{their}\:{respective}\:{disciplines}\:{qualified} \\ $$$${for}\:{an}\:{award}.\:{In}\:{how}\:{many}\:{ways}\:{the}\:{aeard} \\ $$$${can}\:{be}\:{made}\:{if}; \\ $$$$\left({i}\right){only}\:{one}\:{scholarship}\:{is}\:{available}\:{in} \\ $$$${each}\:{of}\:{the}\:{disciplines} \\ $$$$\left({ii}\right){only}\:{two}\:{scholarships}\:{are}\:{availablr} \\ $$$${in}\:{each}\:{of}\:{the}\:{disciplines}. \\ $$

Question Number 77103 Answers: 1 Comments: 1

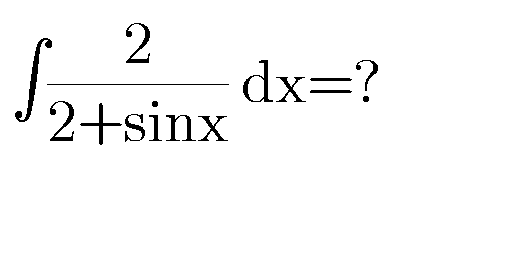
Question Number 77091 Answers: 0 Comments: 3

Question Number 77089 Answers: 0 Comments: 2

Cheap ⇊ ∫(√(x/(√(x/(√(x/(...)))))))dx

$$\boldsymbol{{Cheap}}\:\downdownarrows \\ $$$$\int\sqrt{\frac{\boldsymbol{{x}}}{\sqrt{\frac{\boldsymbol{{x}}}{\sqrt{\frac{\boldsymbol{{x}}}{...}}}}}}\boldsymbol{{dx}} \\ $$$$ \\ $$$$ \\ $$

Question Number 77087 Answers: 1 Comments: 1

∫_0 ^(a/2) x^2 (a^2 −x^2 )^((−3)/2) dx Help!!!

$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{{a}}}{\mathrm{2}}} \boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} \right)^{\frac{−\mathrm{3}}{\mathrm{2}}} \boldsymbol{{dx}} \\ $$$$\boldsymbol{{Help}}!!! \\ $$$$ \\ $$

Question Number 77086 Answers: 1 Comments: 2

∫_0 ^1 xtan^(−1) xdx

$$\int_{\mathrm{0}} ^{\mathrm{1}} {xtan}^{−\mathrm{1}} {xdx} \\ $$$$ \\ $$

Question Number 77067 Answers: 1 Comments: 2

Question Number 77066 Answers: 0 Comments: 5

Question Number 77057 Answers: 1 Comments: 2

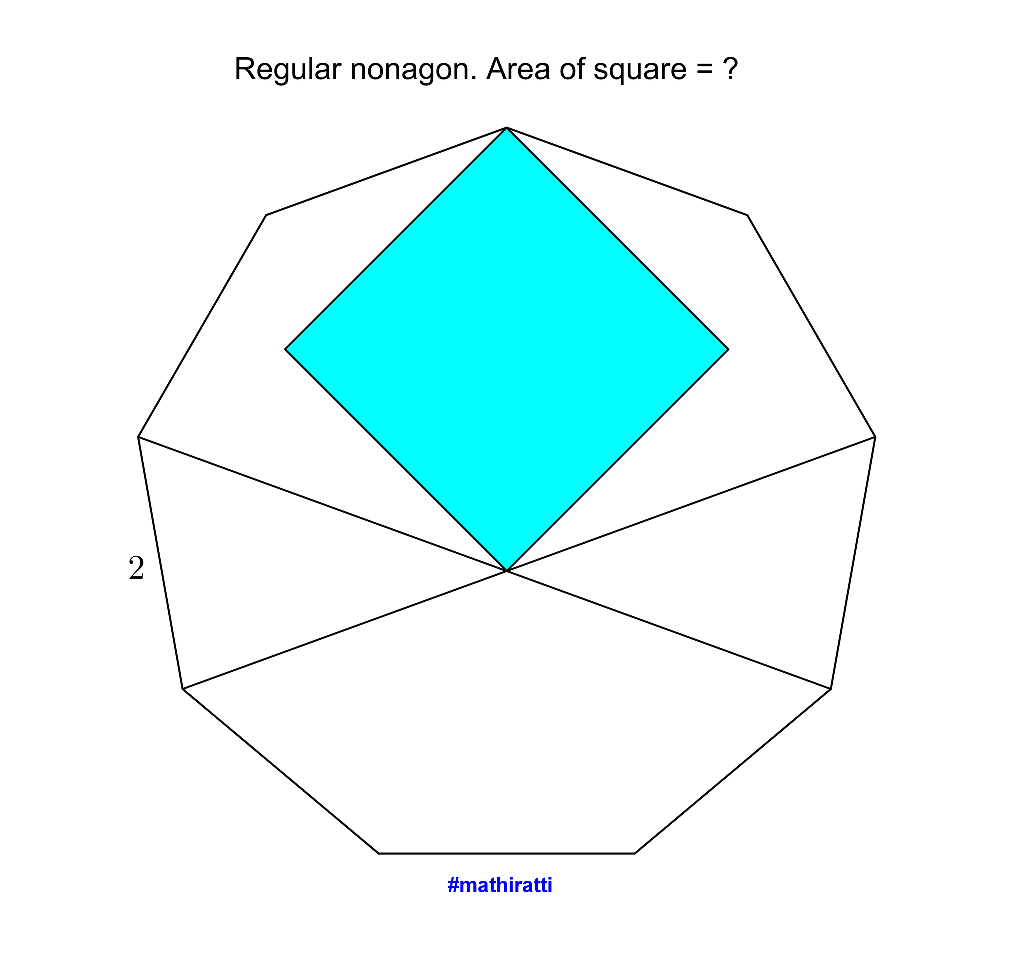
Question Number 77046 Answers: 1 Comments: 0

x=R^2 (√(1−(t^2 /R^2 )))

$${x}={R}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{{R}^{\mathrm{2}} }}\: \\ $$

Question Number 77041 Answers: 2 Comments: 0

solve in [0;π] sinx−sin^3 x=1−cos2x

$$\mathrm{solve}\:\mathrm{in}\:\left[\mathrm{0};\pi\right] \\ $$$$\mathrm{sin}{x}−\mathrm{sin}^{\mathrm{3}} {x}=\mathrm{1}−\mathrm{cos2}{x} \\ $$

Question Number 77036 Answers: 0 Comments: 12

Question Number 77035 Answers: 1 Comments: 0

Solve for x in: (i) (2(x+3)−3(x−2))(2x−1)≥0 (ii)(x−1)(2x+3)(x+1)(x+3)≤1

$${Solve}\:{for}\:{x}\:{in}: \\ $$$$\left({i}\right)\:\left(\mathrm{2}\left({x}+\mathrm{3}\right)−\mathrm{3}\left({x}−\mathrm{2}\right)\right)\left(\mathrm{2}{x}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\left({ii}\right)\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\leqslant\mathrm{1} \\ $$

Question Number 77033 Answers: 0 Comments: 1

Suppose the population models of London and Hongkong in tens of thousands are p(t)=((20t)/(t+1)) and q(t)=((240t)/(t+8)) respectively for t years after 2015, Determine the time period in years when the population of London exceeds that of HongKong.

$${Suppose}\:{the}\:{population}\:{models}\:{of}\:{London} \\ $$$${and}\:{Hongkong}\:{in}\:{tens}\:{of}\:{thousands}\:{are} \\ $$$${p}\left({t}\right)=\frac{\mathrm{20}{t}}{{t}+\mathrm{1}}\:{and}\:{q}\left({t}\right)=\frac{\mathrm{240}{t}}{{t}+\mathrm{8}}\:{respectively}\:{for} \\ $$$${t}\:{years}\:{after}\:\mathrm{2015},\:{Determine}\:{the}\:{time}\:{period} \\ $$$${in}\:{years}\:{when}\:{the}\:{population}\:{of}\:{London} \\ $$$${exceeds}\:{that}\:{of}\:{HongKong}. \\ $$

Question Number 77028 Answers: 1 Comments: 0

Question Number 77027 Answers: 1 Comments: 0

Please help me to solve it in [−π;0] cos2x+cosx+1=sin3x+sin2x+sinx Explain details if possible.

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{in}\:\left[−\pi;\mathrm{0}\right] \\ $$$$\mathrm{cos2}{x}+\mathrm{cos}{x}+\mathrm{1}=\mathrm{sin3}{x}+\mathrm{sin2}{x}+\mathrm{sin}{x} \\ $$$${E}\mathrm{xplain}\:\mathrm{details}\:\mathrm{if}\:\mathrm{possible}. \\ $$$$ \\ $$

Question Number 77026 Answers: 2 Comments: 2

Question Number 77024 Answers: 1 Comments: 0

The possible value of p for which graph of the function f(x)=2p^2 − 3ptan x+tan^2 x+1 does not lie below x-axis for all x∈(((−Π)/2),(Π/2)) is (a)0 (b)4 (c)3 (d)8

$$\mathrm{The}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{p}\:\mathrm{for}\:\mathrm{which}\: \\ $$$$\mathrm{graph}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2p}^{\mathrm{2}} − \\ $$$$\mathrm{3ptan}\:\mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\:\mathrm{does}\:\mathrm{not}\:\mathrm{lie}\:\mathrm{below}\: \\ $$$$\mathrm{x}-\mathrm{axis}\:\mathrm{for}\:\mathrm{all}\:\mathrm{x}\in\left(\frac{−\Pi}{\mathrm{2}},\frac{\Pi}{\mathrm{2}}\right)\:\mathrm{is} \\ $$$$\left(\mathrm{a}\right)\mathrm{0}\:\:\:\:\:\:\left(\mathrm{b}\right)\mathrm{4}\:\:\:\:\:\:\:\:\left(\mathrm{c}\right)\mathrm{3}\:\:\:\:\:\:\:\:\left(\mathrm{d}\right)\mathrm{8} \\ $$

Question Number 77015 Answers: 0 Comments: 1

Question Number 77014 Answers: 0 Comments: 3

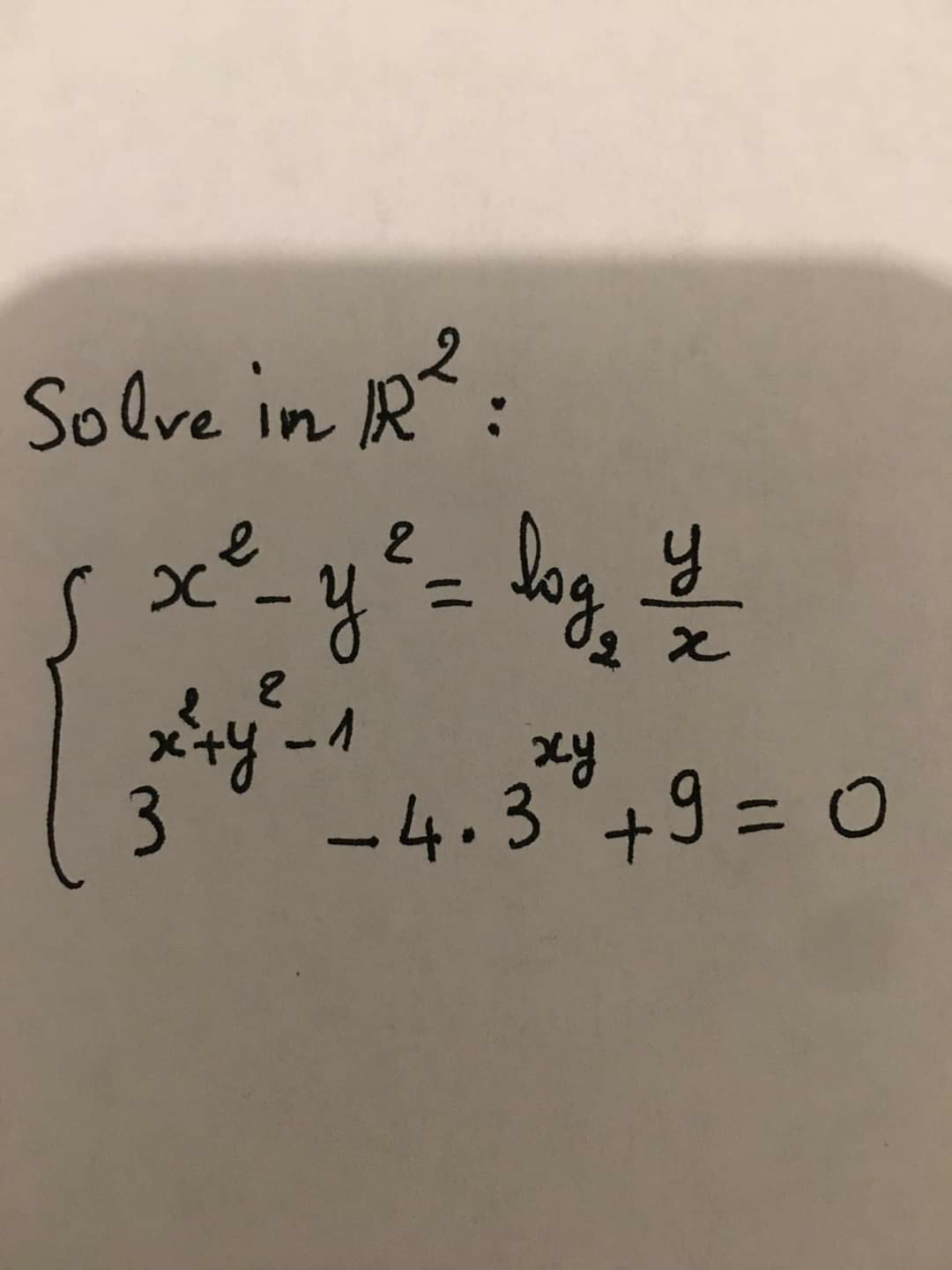
Question Number 77009 Answers: 0 Comments: 4

Question Number 77002 Answers: 2 Comments: 2

calculate ∫ (dt/(cos (2t+a)cos (2t−a)))

$$ \\ $$$${calculate}\:\int\:\frac{{dt}}{\mathrm{cos}\:\left(\mathrm{2}{t}+{a}\right)\mathrm{cos}\:\left(\mathrm{2}{t}−{a}\right)} \\ $$

Question Number 77001 Answers: 1 Comments: 0

The point (4,1) undergoes the following two successive transformations (i) reflection about the line y=x (ii) translation through a distance 2 units along the positive x axis then find the final coordinates of the point ????

$$\mathrm{The}\:\mathrm{point}\:\left(\mathrm{4},\mathrm{1}\right)\:\mathrm{undergoes}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{two}\:\mathrm{successive}\:\mathrm{transformations} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{reflection}\:\mathrm{about}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{x} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{translation}\:\mathrm{through}\:\mathrm{a}\:\mathrm{distance} \\ $$$$\mathrm{2}\:\mathrm{units}\:\mathrm{along}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{x}\:\mathrm{axis} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{final}\:\mathrm{coordinates} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:???? \\ $$

Question Number 77000 Answers: 1 Comments: 1

One vertex of the equalateral triangle with centroid at the origin and one side as x+y−2 = 0 is (a) (−1,−1) (b) (2,2) (c) (−2,−2) (d) (2,−2)

$$\mathrm{One}\:\mathrm{vertex}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equalateral}\:\mathrm{triangle} \\ $$$$\mathrm{with}\:\mathrm{centroid}\:\mathrm{at}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{and}\:\mathrm{one} \\ $$$$\mathrm{side}\:\mathrm{as}\:\mathrm{x}+\mathrm{y}−\mathrm{2}\:=\:\mathrm{0}\:\mathrm{is} \\ $$$$\left(\mathrm{a}\right)\:\:\left(−\mathrm{1},−\mathrm{1}\right)\:\:\left(\mathrm{b}\right)\:\left(\mathrm{2},\mathrm{2}\right)\:\:\left(\mathrm{c}\right)\:\left(−\mathrm{2},−\mathrm{2}\right) \\ $$$$\left(\mathrm{d}\right)\:\left(\mathrm{2},−\mathrm{2}\right) \\ $$

Question Number 76995 Answers: 0 Comments: 0

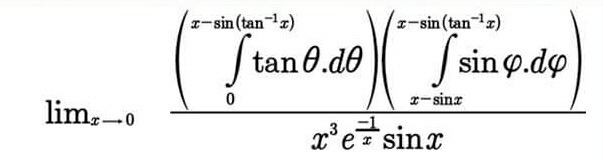
Question Number 76991 Answers: 1 Comments: 1

Pg 1362 Pg 1363 Pg 1364 Pg 1365 Pg 1366 Pg 1367 Pg 1368 Pg 1369 Pg 1370 Pg 1371

Contact: [email protected]