
AllQuestion and Answers: Page 1354
Question Number 78266 Answers: 1 Comments: 2
Question Number 78264 Answers: 0 Comments: 4
Question Number 78263 Answers: 1 Comments: 2
Question Number 78265 Answers: 1 Comments: 0
$${find}\:\int\:\:\frac{{sin}^{\mathrm{3}} {x}}{{tan}^{\mathrm{5}} {x}}{dx} \\ $$
Question Number 78256 Answers: 0 Comments: 0
Question Number 78261 Answers: 0 Comments: 3
Question Number 78251 Answers: 1 Comments: 0
$$\int\frac{{x}+\mathrm{4}}{{x}−\sqrt[{\mathrm{3}}]{{x}}}\:{dx}\: \\ $$
Question Number 78246 Answers: 0 Comments: 0
Question Number 78233 Answers: 0 Comments: 8
$${given}\:\mathrm{5}{x}+\mathrm{22}{y}=\mathrm{18} \\ $$$${find}\:{for}\:{x},{y}\:{integer} \\ $$
Question Number 78216 Answers: 1 Comments: 5
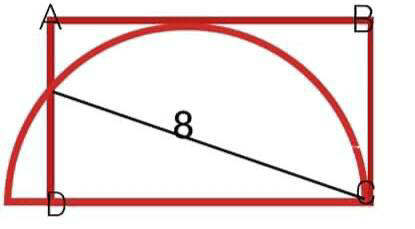
Question Number 78207 Answers: 1 Comments: 6
Question Number 78198 Answers: 1 Comments: 4

Question Number 78177 Answers: 1 Comments: 10
Question Number 78168 Answers: 0 Comments: 6
Question Number 78163 Answers: 0 Comments: 2
Question Number 78162 Answers: 0 Comments: 4
Question Number 78161 Answers: 1 Comments: 0

Question Number 78160 Answers: 0 Comments: 1
Question Number 78156 Answers: 0 Comments: 1
Question Number 78153 Answers: 1 Comments: 1

Question Number 78147 Answers: 0 Comments: 0

Question Number 78136 Answers: 1 Comments: 5
Question Number 78135 Answers: 0 Comments: 0
Question Number 78134 Answers: 0 Comments: 1
Question Number 78122 Answers: 1 Comments: 3
Question Number 78119 Answers: 1 Comments: 6
Pg 1349 Pg 1350 Pg 1351 Pg 1352 Pg 1353 Pg 1354 Pg 1355 Pg 1356 Pg 1357 Pg 1358
