
AllQuestion and Answers: Page 1352
Question Number 79051 Answers: 0 Comments: 1
Question Number 79049 Answers: 0 Comments: 0
Question Number 79055 Answers: 0 Comments: 3
Question Number 79052 Answers: 0 Comments: 0
Question Number 79054 Answers: 0 Comments: 0
Question Number 79053 Answers: 0 Comments: 0
Question Number 79026 Answers: 4 Comments: 5

Question Number 79015 Answers: 0 Comments: 4
Question Number 79010 Answers: 1 Comments: 0
Question Number 79004 Answers: 2 Comments: 3
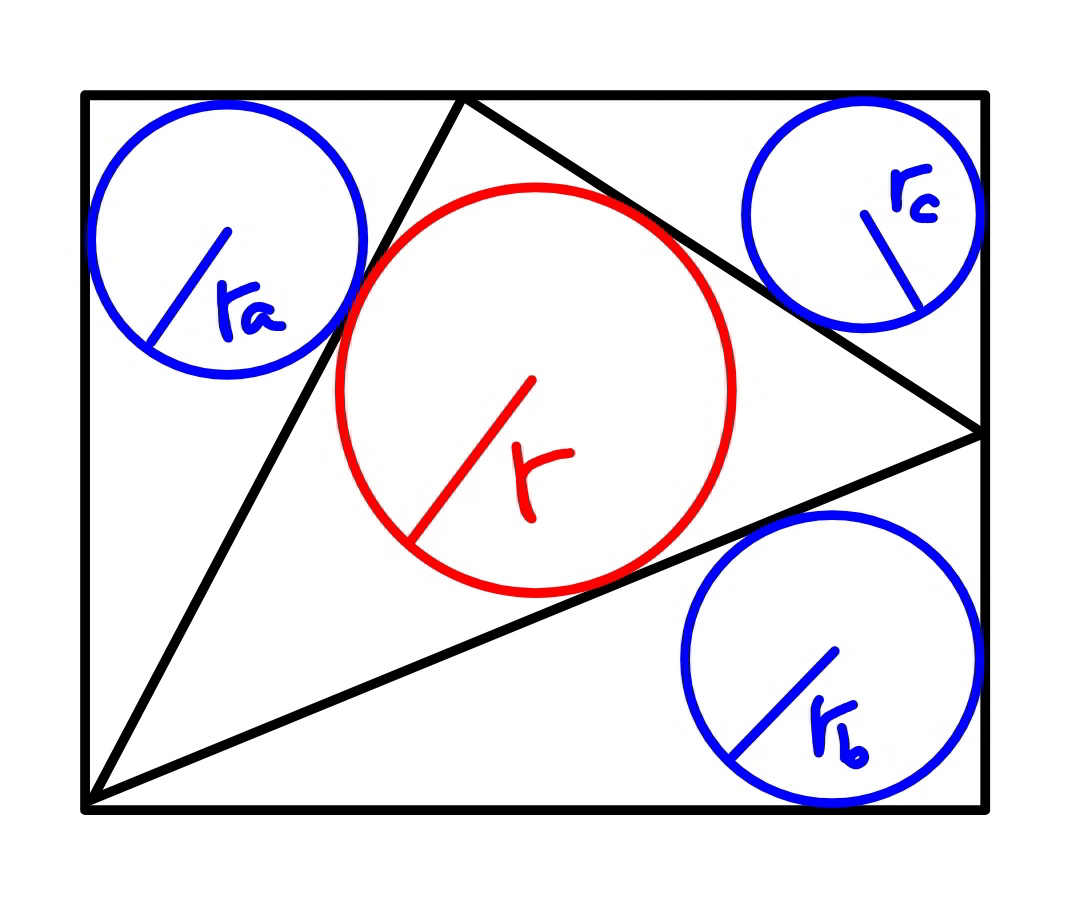
Question Number 79001 Answers: 0 Comments: 3
Question Number 79000 Answers: 0 Comments: 2
Question Number 78999 Answers: 1 Comments: 2
Question Number 78998 Answers: 0 Comments: 0
Question Number 78979 Answers: 0 Comments: 4
Question Number 78974 Answers: 3 Comments: 3
Question Number 78948 Answers: 1 Comments: 7
Question Number 78946 Answers: 1 Comments: 2
$$\mathrm{solve} \\ $$$$\mathrm{cos}{x}−\sqrt{\mathrm{3}}{sinx}=\mathrm{1} \\ $$
Question Number 78944 Answers: 0 Comments: 1
Question Number 78941 Answers: 2 Comments: 0
Question Number 78937 Answers: 1 Comments: 5

Question Number 78933 Answers: 0 Comments: 4

Question Number 78931 Answers: 1 Comments: 8
Question Number 78897 Answers: 1 Comments: 11
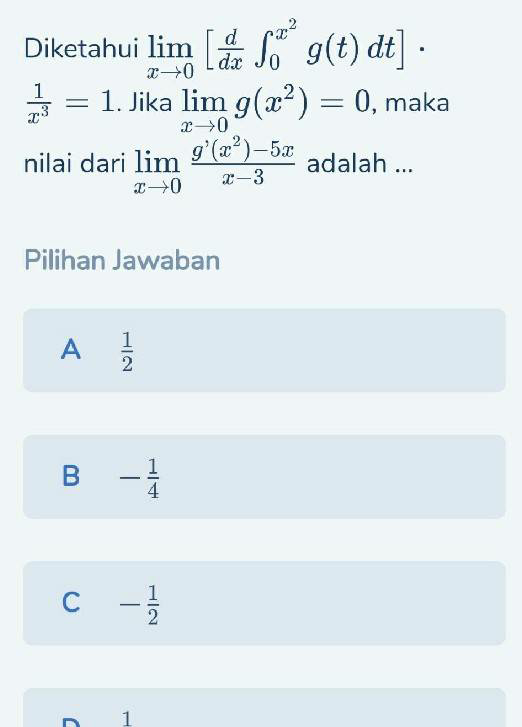
Question Number 78894 Answers: 0 Comments: 1
Question Number 78890 Answers: 0 Comments: 2
Pg 1347 Pg 1348 Pg 1349 Pg 1350 Pg 1351 Pg 1352 Pg 1353 Pg 1354 Pg 1355 Pg 1356
