
AllQuestion and Answers: Page 1349
Question Number 78894 Answers: 0 Comments: 1
Question Number 78890 Answers: 0 Comments: 2
Question Number 78889 Answers: 1 Comments: 0
Question Number 78888 Answers: 1 Comments: 1
Question Number 78887 Answers: 0 Comments: 2
Question Number 78885 Answers: 1 Comments: 0
Question Number 78878 Answers: 1 Comments: 0
Question Number 78877 Answers: 1 Comments: 6
Question Number 78880 Answers: 1 Comments: 0
Question Number 78865 Answers: 2 Comments: 5
Question Number 78857 Answers: 1 Comments: 5
Question Number 78853 Answers: 4 Comments: 0
Question Number 78851 Answers: 0 Comments: 1

Question Number 78829 Answers: 0 Comments: 8
Question Number 78828 Answers: 0 Comments: 3
Question Number 78827 Answers: 0 Comments: 2
Question Number 78815 Answers: 1 Comments: 0
Question Number 78814 Answers: 1 Comments: 1

Question Number 78820 Answers: 1 Comments: 0
Question Number 78800 Answers: 1 Comments: 3
Question Number 78799 Answers: 1 Comments: 3
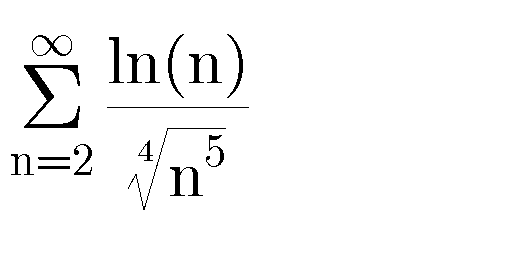
Question Number 78797 Answers: 1 Comments: 0
Question Number 78794 Answers: 1 Comments: 0
Question Number 78791 Answers: 1 Comments: 0
Question Number 78785 Answers: 1 Comments: 0
Question Number 78770 Answers: 0 Comments: 0
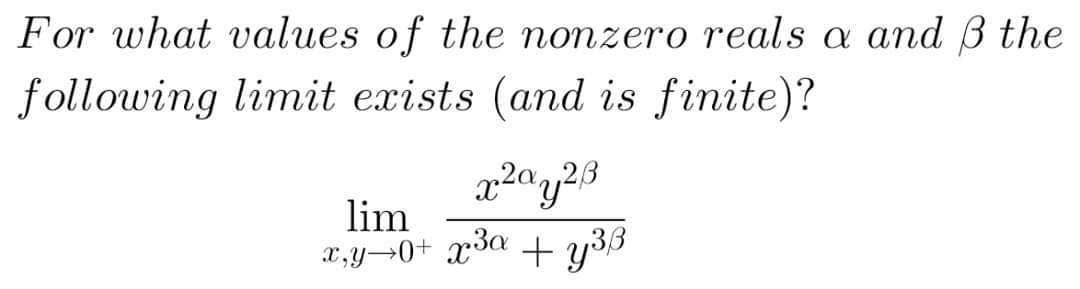
Pg 1344 Pg 1345 Pg 1346 Pg 1347 Pg 1348 Pg 1349 Pg 1350 Pg 1351 Pg 1352 Pg 1353
