
AllQuestion and Answers: Page 1348
Question Number 79516 Answers: 0 Comments: 3

Question Number 79515 Answers: 0 Comments: 0

Question Number 79513 Answers: 0 Comments: 1
Question Number 79512 Answers: 0 Comments: 0
Question Number 79852 Answers: 2 Comments: 1

Question Number 79500 Answers: 1 Comments: 0
$$\int\left(\mathrm{cot}\:^{\mathrm{2}} {x}+\mathrm{cot}\:^{\mathrm{4}} {x}\right){dx} \\ $$
Question Number 79499 Answers: 0 Comments: 2
Question Number 79491 Answers: 0 Comments: 4
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{used}\:\mathrm{place} \\ $$
Question Number 79485 Answers: 1 Comments: 0
$$\int\left(\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{tan}\:^{\mathrm{4}} {x}\right){dx} \\ $$
Question Number 79480 Answers: 0 Comments: 3

Question Number 79479 Answers: 0 Comments: 1
Question Number 79497 Answers: 1 Comments: 0
Question Number 79472 Answers: 0 Comments: 5
Question Number 79469 Answers: 0 Comments: 0
Question Number 79462 Answers: 1 Comments: 0
Question Number 79456 Answers: 0 Comments: 2
Question Number 79455 Answers: 1 Comments: 0
Question Number 79453 Answers: 1 Comments: 0
Question Number 79452 Answers: 1 Comments: 1
Question Number 79449 Answers: 1 Comments: 6
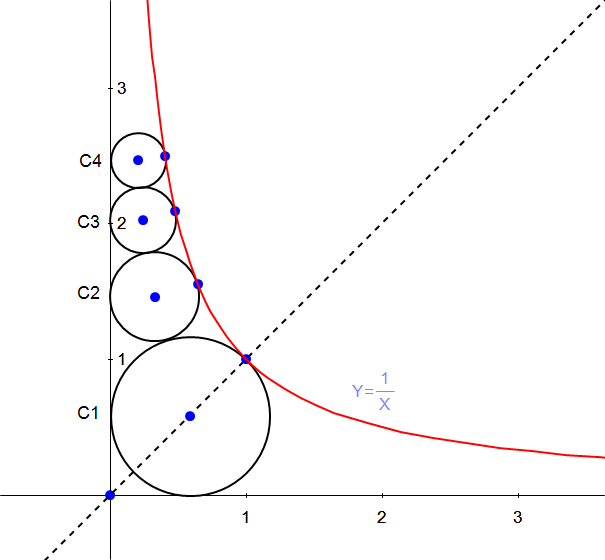
Question Number 79443 Answers: 1 Comments: 1
Question Number 79437 Answers: 0 Comments: 2
Question Number 79435 Answers: 0 Comments: 1
Question Number 79424 Answers: 0 Comments: 0
Question Number 79423 Answers: 1 Comments: 0
Question Number 79419 Answers: 0 Comments: 6
Pg 1343 Pg 1344 Pg 1345 Pg 1346 Pg 1347 Pg 1348 Pg 1349 Pg 1350 Pg 1351 Pg 1352
