
AllQuestion and Answers: Page 1345
Question Number 79929 Answers: 0 Comments: 0
Question Number 79913 Answers: 0 Comments: 1
Question Number 79903 Answers: 1 Comments: 11

Question Number 79883 Answers: 0 Comments: 9
Question Number 79879 Answers: 1 Comments: 5

Question Number 79876 Answers: 1 Comments: 1
Question Number 79964 Answers: 0 Comments: 3
Question Number 79947 Answers: 0 Comments: 4
Question Number 79946 Answers: 2 Comments: 0
Question Number 79943 Answers: 1 Comments: 5
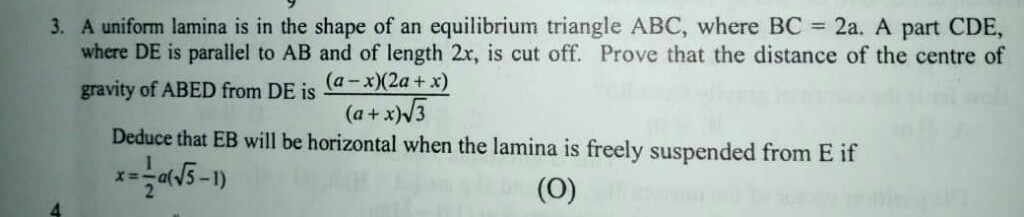
Question Number 79869 Answers: 0 Comments: 1
Question Number 79866 Answers: 0 Comments: 1
Question Number 79864 Answers: 0 Comments: 0

Question Number 79861 Answers: 0 Comments: 1

Question Number 79856 Answers: 0 Comments: 2

Question Number 79838 Answers: 1 Comments: 0
Question Number 79837 Answers: 1 Comments: 10
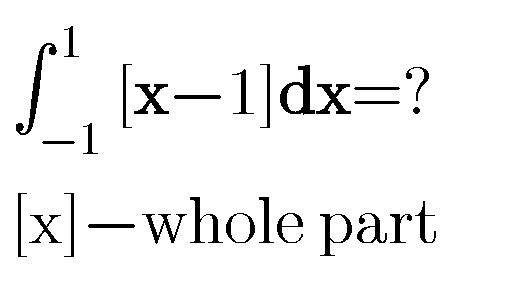
Question Number 79826 Answers: 0 Comments: 7
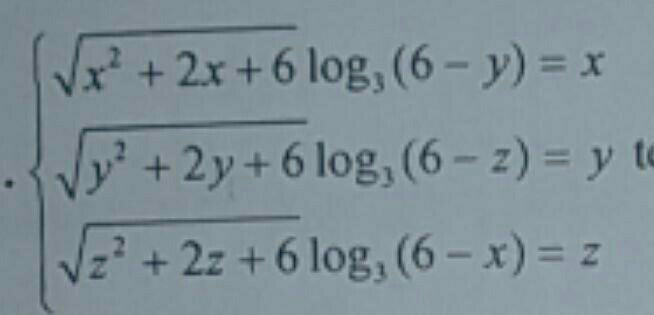
Question Number 79825 Answers: 0 Comments: 4
Question Number 79824 Answers: 2 Comments: 7

Question Number 79816 Answers: 1 Comments: 0
Question Number 79814 Answers: 0 Comments: 5
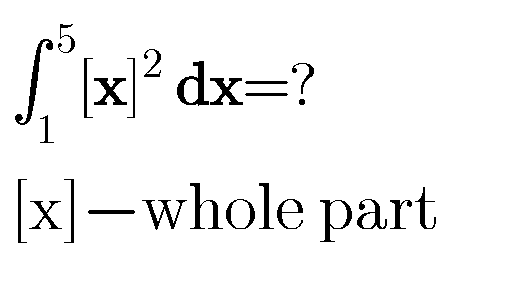
Question Number 79807 Answers: 2 Comments: 2

Question Number 79798 Answers: 0 Comments: 7
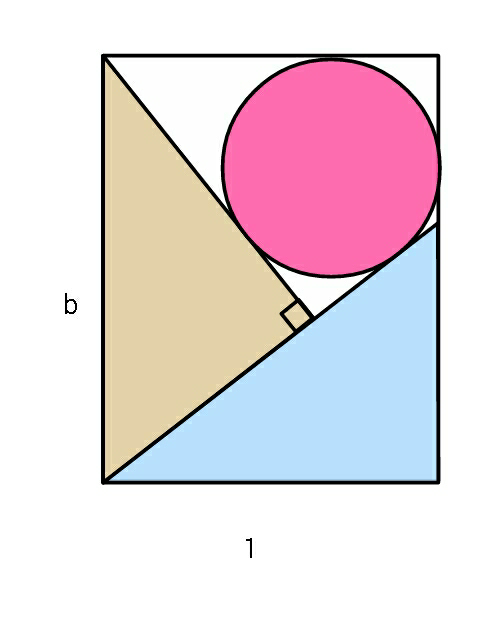
Question Number 79794 Answers: 1 Comments: 2

Question Number 79792 Answers: 1 Comments: 1
Pg 1340 Pg 1341 Pg 1342 Pg 1343 Pg 1344 Pg 1345 Pg 1346 Pg 1347 Pg 1348 Pg 1349
