
AllQuestion and Answers: Page 1344
Question Number 80093 Answers: 3 Comments: 0
Question Number 80088 Answers: 0 Comments: 0
Question Number 80084 Answers: 0 Comments: 3
Question Number 80068 Answers: 2 Comments: 3

Question Number 80065 Answers: 0 Comments: 0

Question Number 80064 Answers: 1 Comments: 6
Question Number 80057 Answers: 1 Comments: 2

Question Number 80053 Answers: 0 Comments: 4
Question Number 80052 Answers: 0 Comments: 0
Question Number 80108 Answers: 1 Comments: 3
Question Number 80039 Answers: 1 Comments: 6
Question Number 80037 Answers: 0 Comments: 0
Question Number 80036 Answers: 1 Comments: 3
Question Number 80027 Answers: 0 Comments: 4
Question Number 80015 Answers: 2 Comments: 2
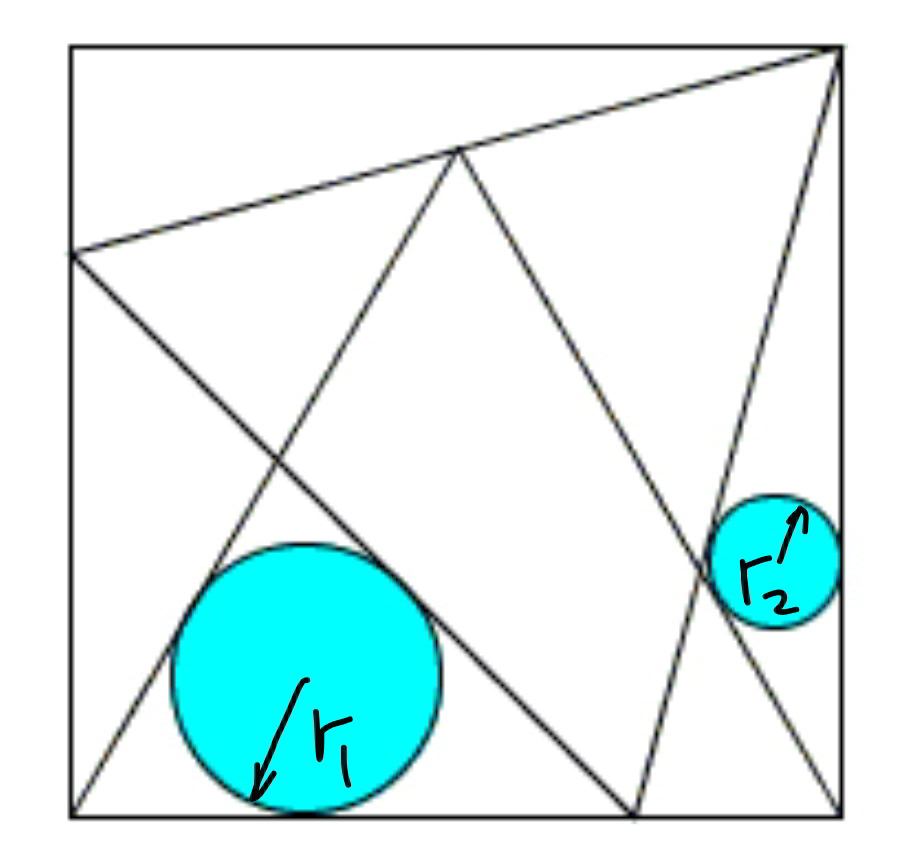
Question Number 79992 Answers: 0 Comments: 2
Question Number 80000 Answers: 1 Comments: 2
Question Number 79998 Answers: 0 Comments: 3
Question Number 79978 Answers: 3 Comments: 0
Question Number 79974 Answers: 1 Comments: 0

Question Number 80004 Answers: 1 Comments: 2
Question Number 79969 Answers: 1 Comments: 0
Question Number 79968 Answers: 0 Comments: 3
$${Find}\:{the}\:\mathrm{50}^{{th}} \:{entry}\:{of}\:\:\mathrm{3}.\mathrm{127356432}... \\ $$
Question Number 79966 Answers: 1 Comments: 1

Question Number 79950 Answers: 0 Comments: 3
Question Number 79932 Answers: 1 Comments: 1

Pg 1339 Pg 1340 Pg 1341 Pg 1342 Pg 1343 Pg 1344 Pg 1345 Pg 1346 Pg 1347 Pg 1348
