
AllQuestion and Answers: Page 1343
Question Number 79649 Answers: 1 Comments: 6
Question Number 79647 Answers: 1 Comments: 2
Question Number 79646 Answers: 0 Comments: 1
Question Number 79645 Answers: 0 Comments: 0
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}^{\mathrm{4}} \right){dx} \\ $$
Question Number 79644 Answers: 1 Comments: 1
Question Number 79635 Answers: 0 Comments: 9
Question Number 79634 Answers: 1 Comments: 3
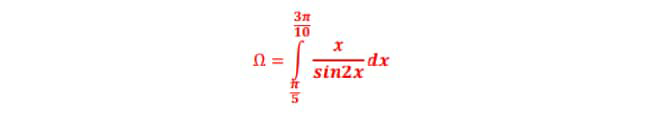
Question Number 79627 Answers: 0 Comments: 2
Question Number 79626 Answers: 1 Comments: 0
Question Number 79625 Answers: 1 Comments: 0
Question Number 79615 Answers: 0 Comments: 3
Question Number 79609 Answers: 1 Comments: 1

Question Number 79607 Answers: 0 Comments: 1
Question Number 79588 Answers: 1 Comments: 3
Question Number 79580 Answers: 0 Comments: 5
Question Number 79572 Answers: 1 Comments: 1
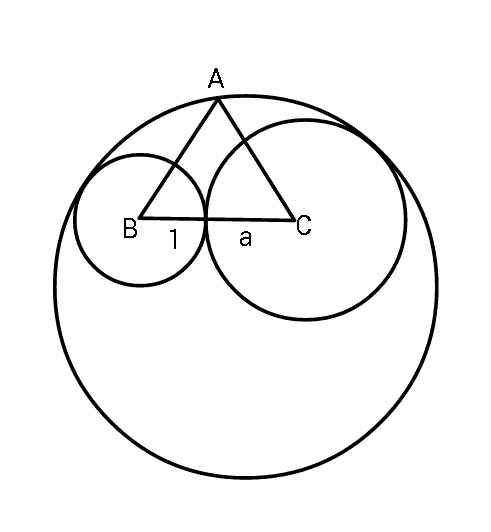
Question Number 79571 Answers: 1 Comments: 5
Question Number 79613 Answers: 1 Comments: 0
Question Number 79612 Answers: 1 Comments: 0
Question Number 79565 Answers: 0 Comments: 2
Question Number 79560 Answers: 0 Comments: 1
$$\sqrt{\mathrm{1}+\mathrm{x}}\:\leqslant\:\sqrt[{\mathrm{4}\:}]{\mathrm{5}−\mathrm{x}} \\ $$
Question Number 79538 Answers: 1 Comments: 13
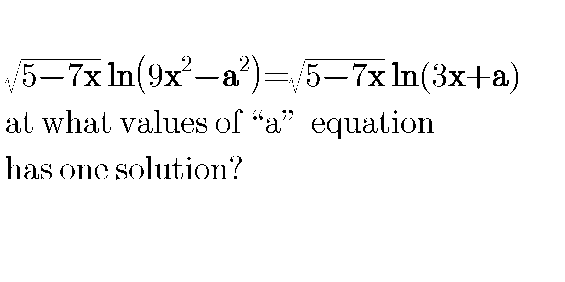
Question Number 79536 Answers: 0 Comments: 4

Question Number 79532 Answers: 1 Comments: 2
Question Number 79531 Answers: 0 Comments: 1
Question Number 79528 Answers: 0 Comments: 0
Pg 1338 Pg 1339 Pg 1340 Pg 1341 Pg 1342 Pg 1343 Pg 1344 Pg 1345 Pg 1346 Pg 1347
