
AllQuestion and Answers: Page 1341
Question Number 80540 Answers: 0 Comments: 1

Question Number 80539 Answers: 0 Comments: 1

Question Number 80529 Answers: 0 Comments: 1

Question Number 80519 Answers: 2 Comments: 2
Question Number 80515 Answers: 0 Comments: 1
$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\phi} \right)^{\phi} } \\ $$
Question Number 80508 Answers: 0 Comments: 4
Question Number 80505 Answers: 0 Comments: 8
Question Number 80493 Answers: 0 Comments: 4
Question Number 80485 Answers: 0 Comments: 1
Question Number 80477 Answers: 0 Comments: 5

Question Number 80475 Answers: 0 Comments: 0
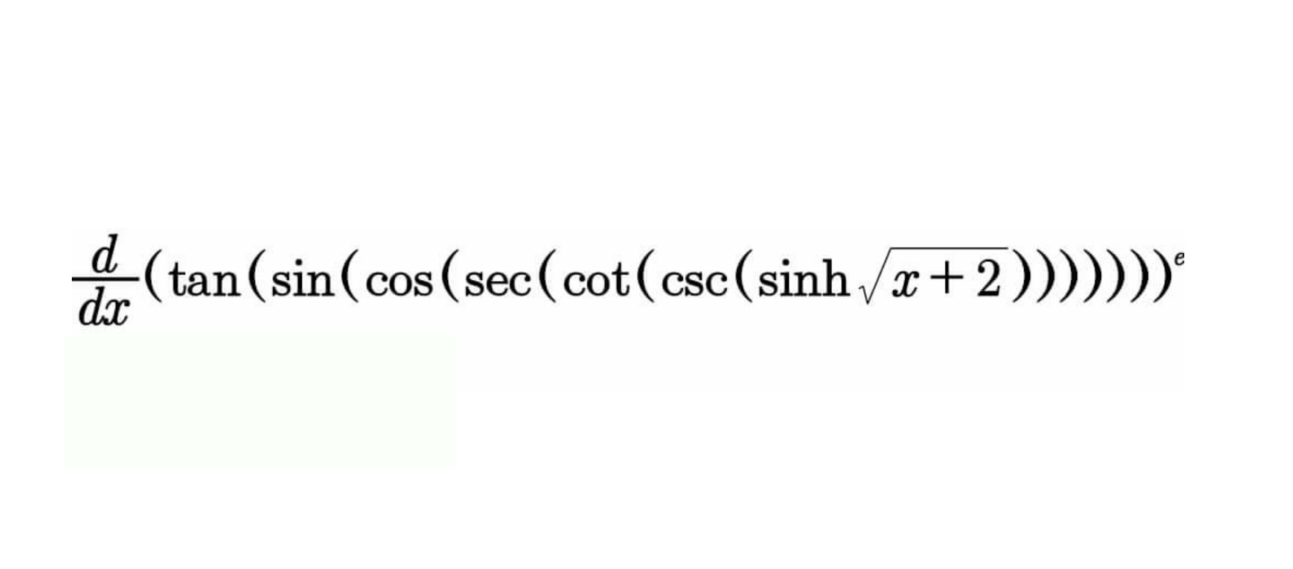
Question Number 80503 Answers: 1 Comments: 0
Question Number 80504 Answers: 0 Comments: 2
Question Number 80501 Answers: 0 Comments: 0
Question Number 80455 Answers: 1 Comments: 2
Question Number 80452 Answers: 0 Comments: 1
Question Number 80451 Answers: 0 Comments: 1
Question Number 80448 Answers: 1 Comments: 3
Question Number 80442 Answers: 1 Comments: 4

Question Number 80433 Answers: 1 Comments: 6
Question Number 80432 Answers: 0 Comments: 7
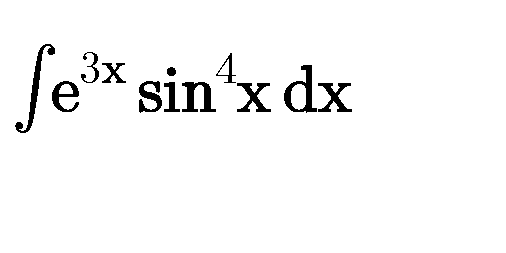
Question Number 80417 Answers: 0 Comments: 5
Question Number 80416 Answers: 1 Comments: 0
Question Number 80405 Answers: 1 Comments: 11
Question Number 80404 Answers: 1 Comments: 0

Question Number 80402 Answers: 0 Comments: 0
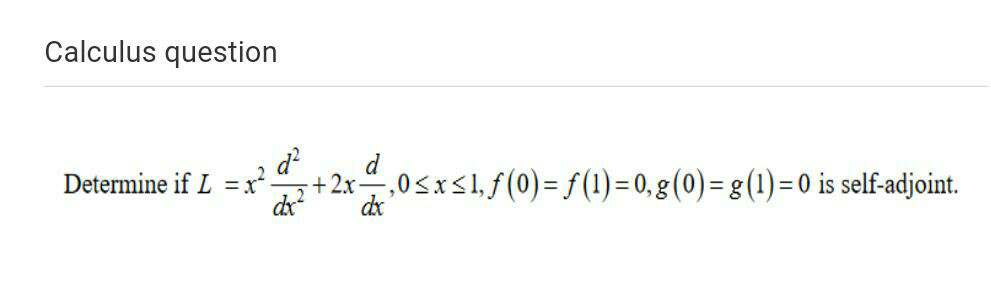
Pg 1336 Pg 1337 Pg 1338 Pg 1339 Pg 1340 Pg 1341 Pg 1342 Pg 1343 Pg 1344 Pg 1345
