
AllQuestion and Answers: Page 1334
Question Number 81439 Answers: 0 Comments: 2
Question Number 81437 Answers: 0 Comments: 1
$$\mathrm{5}\:^{\mathrm{lnx}} \:=\:\mathrm{50}\:−\mathrm{x}^{\mathrm{ln}\:\mathrm{5}} \\ $$$$ \\ $$
Question Number 81435 Answers: 2 Comments: 6
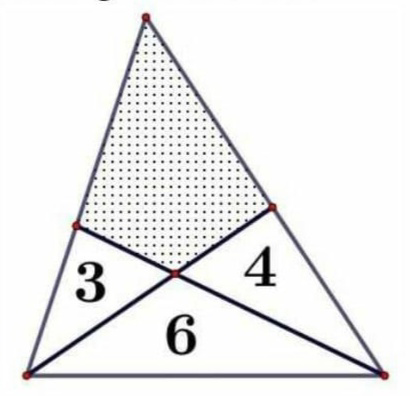
Question Number 81434 Answers: 1 Comments: 2
Question Number 81433 Answers: 1 Comments: 0
Question Number 81432 Answers: 1 Comments: 1
Question Number 81431 Answers: 0 Comments: 2
Question Number 81430 Answers: 0 Comments: 1
Question Number 81429 Answers: 0 Comments: 0
Question Number 81428 Answers: 1 Comments: 0
Question Number 81427 Answers: 1 Comments: 4
Question Number 81421 Answers: 1 Comments: 1
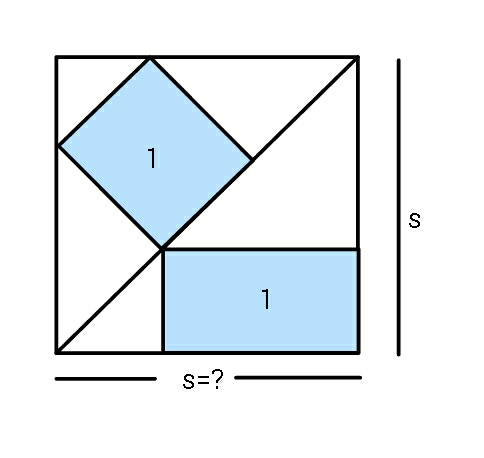
Question Number 81400 Answers: 1 Comments: 3
Question Number 81393 Answers: 2 Comments: 1

Question Number 81404 Answers: 0 Comments: 0

Question Number 81403 Answers: 1 Comments: 1
Question Number 81369 Answers: 2 Comments: 7

Question Number 81364 Answers: 0 Comments: 2
Question Number 81354 Answers: 0 Comments: 2
Question Number 81340 Answers: 1 Comments: 4
Question Number 81336 Answers: 1 Comments: 7
Question Number 81331 Answers: 0 Comments: 10

Question Number 81322 Answers: 1 Comments: 1

Question Number 81320 Answers: 0 Comments: 0

Question Number 81319 Answers: 1 Comments: 0
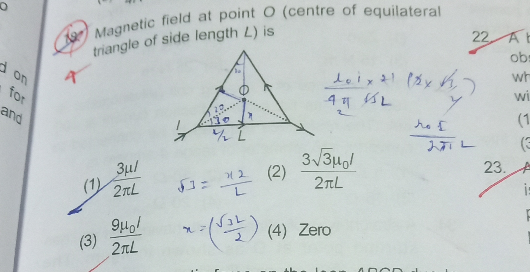
Question Number 81318 Answers: 0 Comments: 1

Pg 1329 Pg 1330 Pg 1331 Pg 1332 Pg 1333 Pg 1334 Pg 1335 Pg 1336 Pg 1337 Pg 1338
