
AllQuestion and Answers: Page 1330
Question Number 81925 Answers: 1 Comments: 0
Question Number 81921 Answers: 1 Comments: 0

Question Number 81911 Answers: 1 Comments: 4

Question Number 81910 Answers: 0 Comments: 1
Question Number 81906 Answers: 0 Comments: 1

Question Number 81889 Answers: 1 Comments: 0

Question Number 81888 Answers: 1 Comments: 1

Question Number 81887 Answers: 0 Comments: 2

Question Number 81884 Answers: 0 Comments: 1

Question Number 81879 Answers: 0 Comments: 2
Question Number 81876 Answers: 0 Comments: 1
Question Number 81892 Answers: 5 Comments: 0

Question Number 81874 Answers: 0 Comments: 2
Question Number 81873 Answers: 1 Comments: 1
Question Number 81872 Answers: 1 Comments: 0
Question Number 81871 Answers: 1 Comments: 3
Question Number 81854 Answers: 1 Comments: 1

Question Number 81853 Answers: 1 Comments: 2
Question Number 81843 Answers: 2 Comments: 5

Question Number 81851 Answers: 0 Comments: 0
Question Number 81836 Answers: 0 Comments: 0

Question Number 81835 Answers: 0 Comments: 1
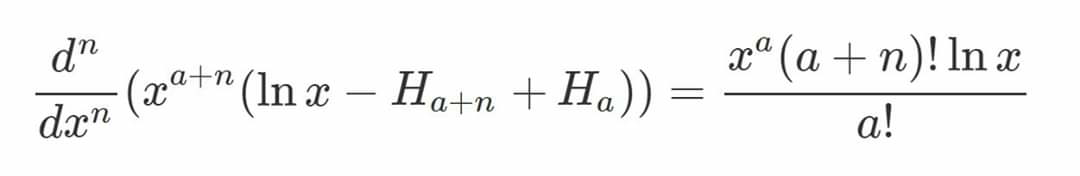
Question Number 81829 Answers: 1 Comments: 2
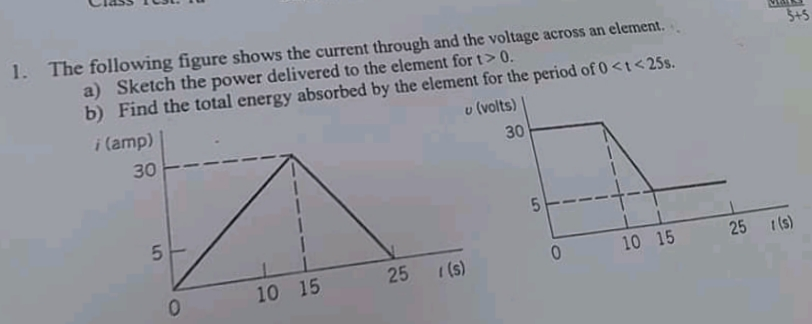
Question Number 81828 Answers: 0 Comments: 0
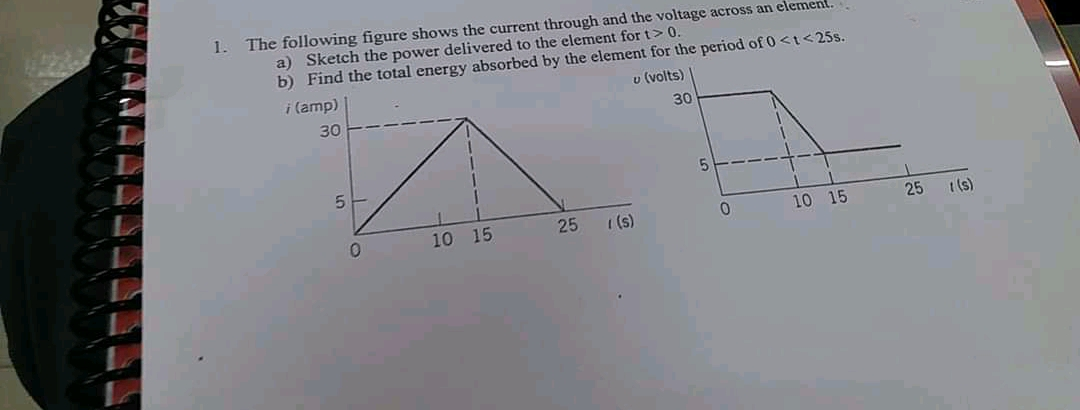
Question Number 81824 Answers: 1 Comments: 0
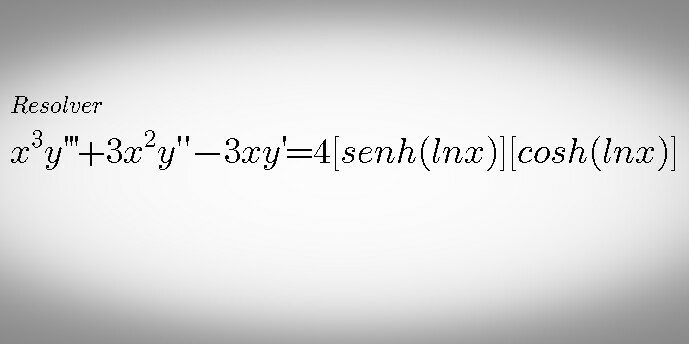
Question Number 81821 Answers: 1 Comments: 0
Pg 1325 Pg 1326 Pg 1327 Pg 1328 Pg 1329 Pg 1330 Pg 1331 Pg 1332 Pg 1333 Pg 1334
