
AllQuestion and Answers: Page 1327
Question Number 82303 Answers: 0 Comments: 18

Question Number 82302 Answers: 0 Comments: 2

Question Number 82290 Answers: 0 Comments: 0
Question Number 82289 Answers: 1 Comments: 4
Question Number 82288 Answers: 0 Comments: 0
Question Number 82287 Answers: 0 Comments: 0
$${find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:\frac{{n}^{{n}} }{{n}!\:{e}^{{n}} } \\ $$
Question Number 82286 Answers: 1 Comments: 3
Question Number 82285 Answers: 0 Comments: 0

Question Number 82284 Answers: 0 Comments: 0

Question Number 82283 Answers: 1 Comments: 2
$$\int{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx} \\ $$
Question Number 82279 Answers: 0 Comments: 0
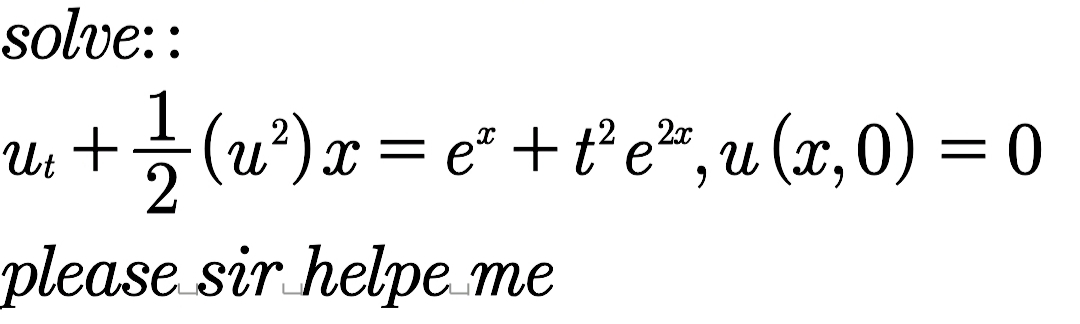
Question Number 82277 Answers: 0 Comments: 4

Question Number 82276 Answers: 0 Comments: 0
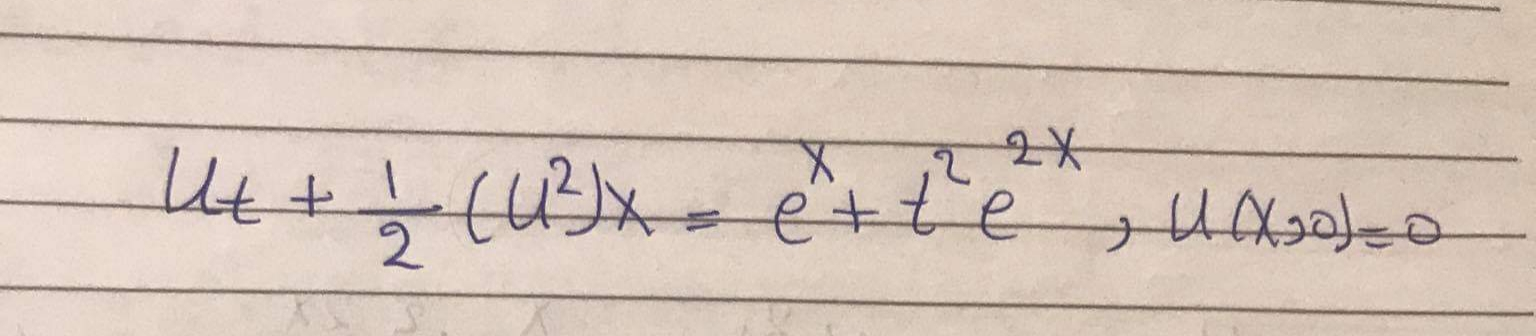
Question Number 82274 Answers: 0 Comments: 0

Question Number 82273 Answers: 0 Comments: 2

Question Number 82390 Answers: 1 Comments: 0
Question Number 82265 Answers: 2 Comments: 0
Question Number 82247 Answers: 1 Comments: 1
Question Number 82245 Answers: 0 Comments: 2
Question Number 82244 Answers: 1 Comments: 2
Question Number 82243 Answers: 1 Comments: 0

Question Number 82232 Answers: 1 Comments: 1

Question Number 82223 Answers: 0 Comments: 1
Question Number 82225 Answers: 0 Comments: 3

Question Number 82191 Answers: 1 Comments: 19
Question Number 82185 Answers: 1 Comments: 2
$$\int\:\frac{{dx}}{\mathrm{sec}\:{x}\:+\:{csc}\:{x}}\:=\:?\: \\ $$
Pg 1322 Pg 1323 Pg 1324 Pg 1325 Pg 1326 Pg 1327 Pg 1328 Pg 1329 Pg 1330 Pg 1331
