
AllQuestion and Answers: Page 1325
Question Number 82514 Answers: 0 Comments: 1
Question Number 82510 Answers: 1 Comments: 1
Question Number 82499 Answers: 1 Comments: 3
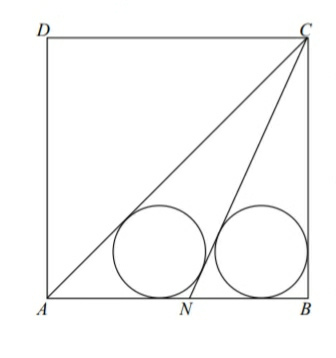
Question Number 82498 Answers: 0 Comments: 0
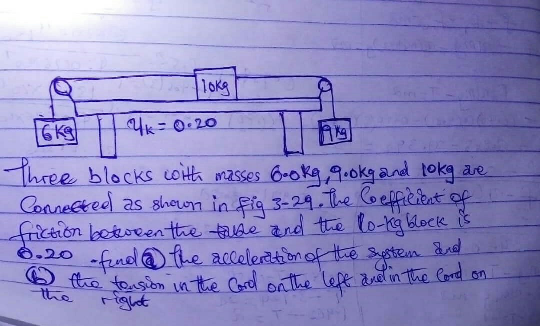
Question Number 82497 Answers: 0 Comments: 0

Question Number 82494 Answers: 0 Comments: 4
Question Number 82489 Answers: 1 Comments: 0
Question Number 82485 Answers: 2 Comments: 4

Question Number 82476 Answers: 1 Comments: 0
Question Number 82474 Answers: 0 Comments: 2
Question Number 82659 Answers: 1 Comments: 3

Question Number 82456 Answers: 0 Comments: 6

Question Number 82452 Answers: 0 Comments: 1
Question Number 82450 Answers: 1 Comments: 1
Question Number 82448 Answers: 0 Comments: 2
Question Number 82447 Answers: 1 Comments: 0
Question Number 82446 Answers: 0 Comments: 3
Question Number 82445 Answers: 1 Comments: 0
Question Number 82440 Answers: 0 Comments: 1
Question Number 82439 Answers: 0 Comments: 1
Question Number 82442 Answers: 0 Comments: 1
Question Number 82435 Answers: 0 Comments: 1
Question Number 82434 Answers: 0 Comments: 0
Question Number 82433 Answers: 0 Comments: 1
Question Number 82431 Answers: 1 Comments: 5
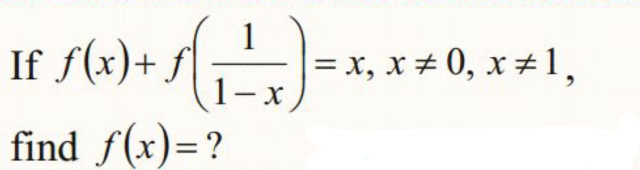
Question Number 82426 Answers: 0 Comments: 2
Pg 1320 Pg 1321 Pg 1322 Pg 1323 Pg 1324 Pg 1325 Pg 1326 Pg 1327 Pg 1328 Pg 1329
