
AllQuestion and Answers: Page 1324
Question Number 82404 Answers: 1 Comments: 7

Question Number 82398 Answers: 0 Comments: 0
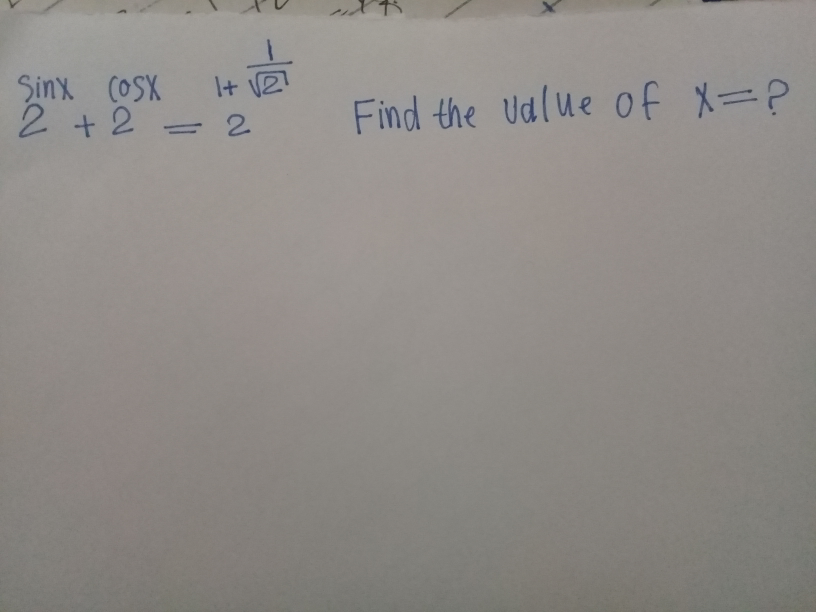
Question Number 82397 Answers: 0 Comments: 2

Question Number 82392 Answers: 0 Comments: 2

Question Number 82391 Answers: 0 Comments: 1
$$\int\:\mathrm{sin}\:{x}\:\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)\:{dx}\:? \\ $$
Question Number 82387 Answers: 0 Comments: 0

Question Number 82386 Answers: 0 Comments: 0
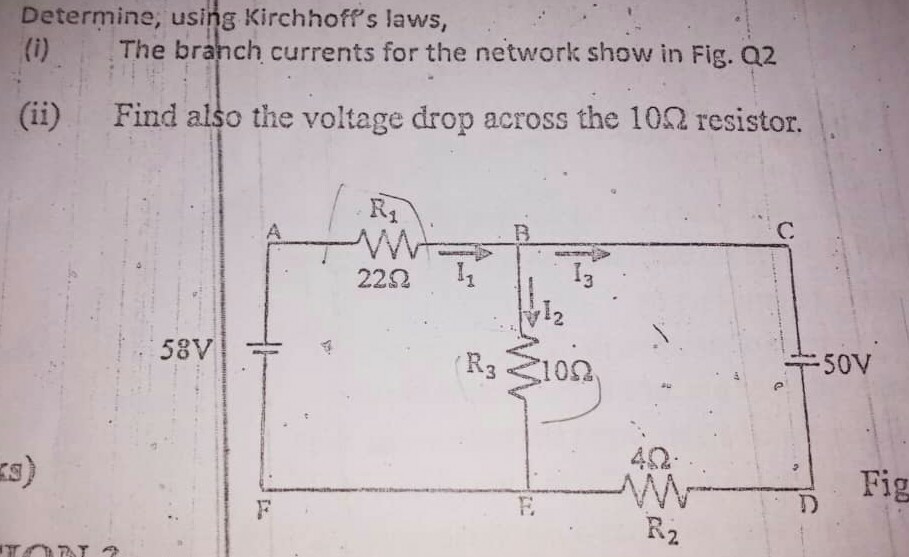
Question Number 82378 Answers: 1 Comments: 1
Question Number 82375 Answers: 2 Comments: 0
Question Number 82365 Answers: 0 Comments: 3

Question Number 82358 Answers: 0 Comments: 3
Question Number 82356 Answers: 0 Comments: 1
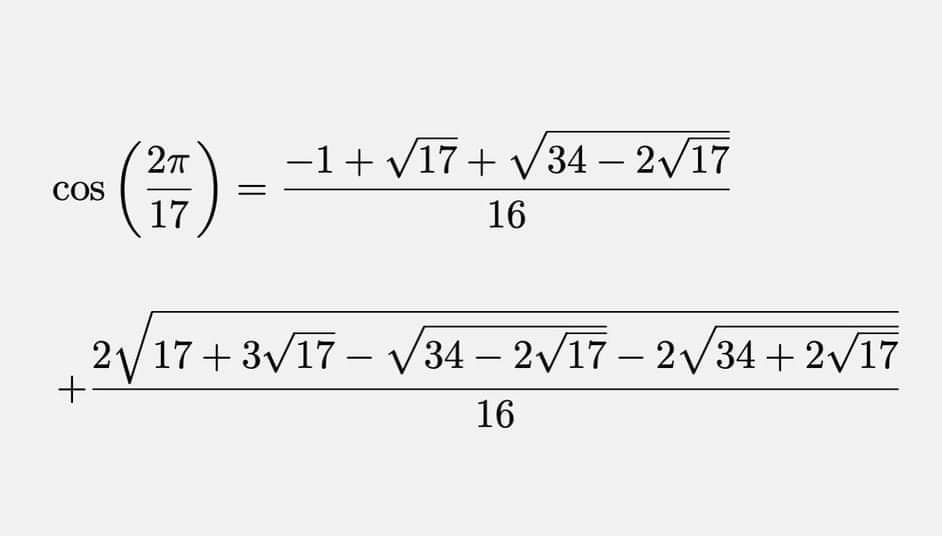
Question Number 82350 Answers: 0 Comments: 1
Question Number 82349 Answers: 1 Comments: 0
Question Number 82339 Answers: 0 Comments: 1

Question Number 82658 Answers: 1 Comments: 2
Question Number 82333 Answers: 0 Comments: 0
$$\left({y}^{\mathrm{4}} −\mathrm{2}{xy}\right)\:{dx}\:=\:−\mathrm{3}{x}^{\mathrm{2}} \:{dy} \\ $$
Question Number 82330 Answers: 0 Comments: 4

Question Number 82308 Answers: 0 Comments: 1

Question Number 82307 Answers: 0 Comments: 3
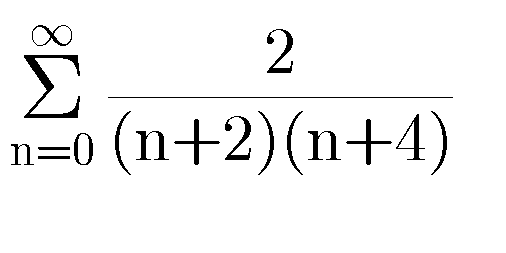
Question Number 82303 Answers: 0 Comments: 18

Question Number 82302 Answers: 0 Comments: 2

Question Number 82290 Answers: 0 Comments: 0
Question Number 82289 Answers: 1 Comments: 4
Question Number 82288 Answers: 0 Comments: 0
Question Number 82287 Answers: 0 Comments: 0
$${find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:\frac{{n}^{{n}} }{{n}!\:{e}^{{n}} } \\ $$
Pg 1319 Pg 1320 Pg 1321 Pg 1322 Pg 1323 Pg 1324 Pg 1325 Pg 1326 Pg 1327 Pg 1328
