
AllQuestion and Answers: Page 1322
Question Number 82867 Answers: 0 Comments: 3
Question Number 82843 Answers: 1 Comments: 0
Question Number 82839 Answers: 0 Comments: 8
Question Number 82877 Answers: 1 Comments: 1
Question Number 82821 Answers: 0 Comments: 1
$${Log}_{{y}} \:{x}+{Log}_{{x}} \:{y}\:=\mathrm{64} \\ $$$${find}\:{x}\:{and}\:{y} \\ $$
Question Number 82806 Answers: 1 Comments: 1
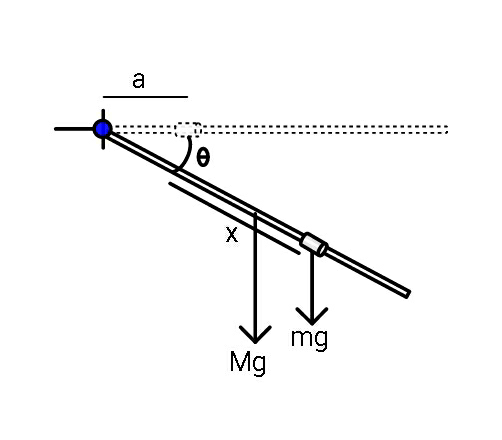
Question Number 82800 Answers: 4 Comments: 2
Question Number 82794 Answers: 0 Comments: 0
Question Number 82792 Answers: 1 Comments: 1
Question Number 82782 Answers: 1 Comments: 1
Question Number 82816 Answers: 0 Comments: 3
Question Number 82815 Answers: 0 Comments: 2
Question Number 82759 Answers: 1 Comments: 0
Question Number 82755 Answers: 1 Comments: 2
Question Number 82753 Answers: 0 Comments: 3
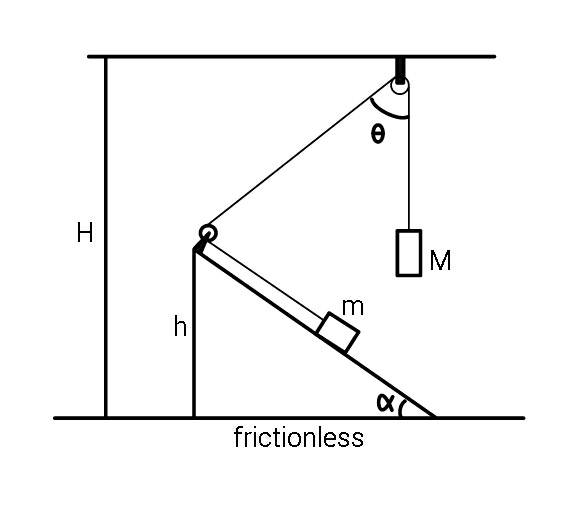
Question Number 82761 Answers: 0 Comments: 7
Question Number 82768 Answers: 0 Comments: 1

Question Number 82767 Answers: 1 Comments: 1
Question Number 82729 Answers: 1 Comments: 2

Question Number 82726 Answers: 0 Comments: 10
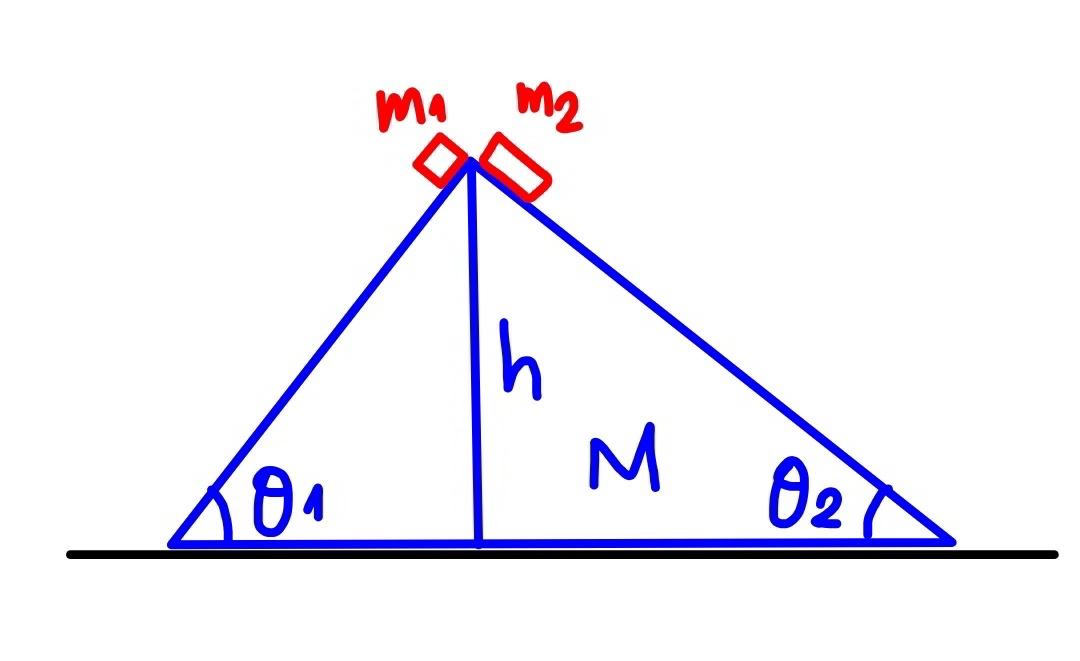
Question Number 82721 Answers: 1 Comments: 2
Question Number 82719 Answers: 2 Comments: 3
Question Number 82701 Answers: 1 Comments: 0
Question Number 82700 Answers: 1 Comments: 4
$$\int\:\frac{\mathrm{2}{dx}}{\mathrm{3}{x}\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{6}}}\:? \\ $$
Question Number 82699 Answers: 0 Comments: 3
Question Number 82687 Answers: 0 Comments: 5

Pg 1317 Pg 1318 Pg 1319 Pg 1320 Pg 1321 Pg 1322 Pg 1323 Pg 1324 Pg 1325 Pg 1326
