
AllQuestion and Answers: Page 1321
Question Number 82991 Answers: 1 Comments: 2

Question Number 82988 Answers: 1 Comments: 3
Question Number 82985 Answers: 1 Comments: 0

Question Number 82975 Answers: 0 Comments: 7
Question Number 82974 Answers: 1 Comments: 1

Question Number 82973 Answers: 0 Comments: 0
Question Number 82972 Answers: 0 Comments: 0
Question Number 82971 Answers: 1 Comments: 2
Question Number 82970 Answers: 0 Comments: 2
Question Number 82954 Answers: 1 Comments: 3
Question Number 82953 Answers: 0 Comments: 3
Question Number 82952 Answers: 1 Comments: 0
Question Number 82944 Answers: 1 Comments: 2
Question Number 82937 Answers: 0 Comments: 2
Question Number 82950 Answers: 1 Comments: 1
Question Number 82929 Answers: 2 Comments: 0
Question Number 82924 Answers: 1 Comments: 2
Question Number 82901 Answers: 1 Comments: 0
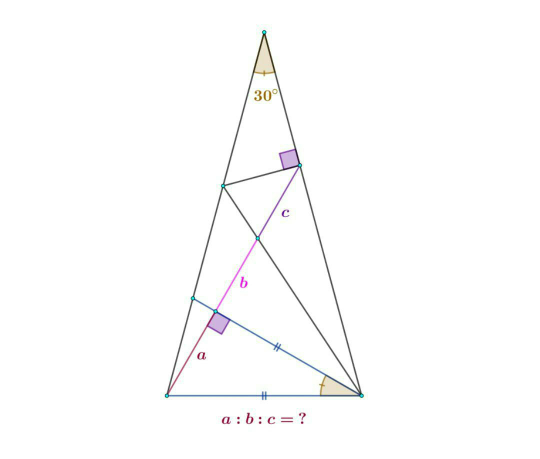
Question Number 82897 Answers: 1 Comments: 2
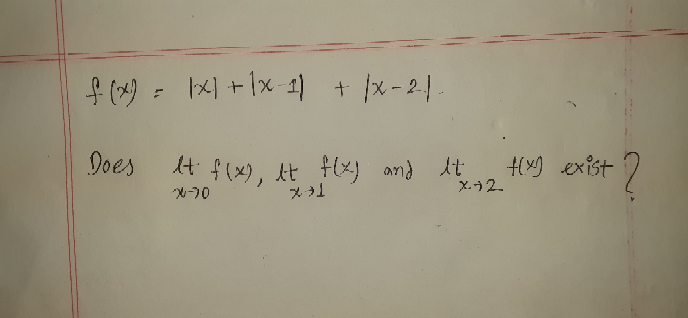
Question Number 82891 Answers: 2 Comments: 0
$$\int\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}\:\mathrm{dx}\:=\:? \\ $$
Question Number 82887 Answers: 1 Comments: 1
Question Number 82886 Answers: 0 Comments: 2
Question Number 82883 Answers: 1 Comments: 0
Question Number 82881 Answers: 1 Comments: 2
Question Number 82879 Answers: 0 Comments: 1
Question Number 82878 Answers: 1 Comments: 3

Pg 1316 Pg 1317 Pg 1318 Pg 1319 Pg 1320 Pg 1321 Pg 1322 Pg 1323 Pg 1324 Pg 1325
