
AllQuestion and Answers: Page 1320
Question Number 83092 Answers: 0 Comments: 0
Question Number 83085 Answers: 1 Comments: 2
Question Number 83078 Answers: 0 Comments: 1
Question Number 83077 Answers: 1 Comments: 0
Question Number 83075 Answers: 1 Comments: 1
Question Number 83074 Answers: 0 Comments: 2
Question Number 83064 Answers: 2 Comments: 0
Question Number 83063 Answers: 1 Comments: 3

Question Number 83050 Answers: 0 Comments: 1

Question Number 83049 Answers: 0 Comments: 0

Question Number 83042 Answers: 0 Comments: 1
Question Number 83037 Answers: 0 Comments: 3
Question Number 83036 Answers: 0 Comments: 3
Question Number 83035 Answers: 1 Comments: 1

Question Number 83032 Answers: 1 Comments: 0
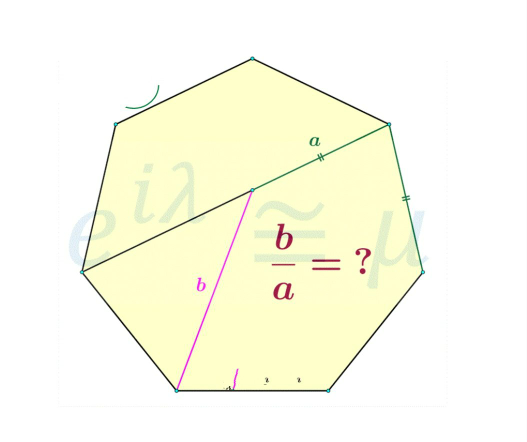
Question Number 83030 Answers: 1 Comments: 0

Question Number 83028 Answers: 0 Comments: 3
Question Number 83026 Answers: 0 Comments: 0
Question Number 83021 Answers: 0 Comments: 0
Question Number 83020 Answers: 0 Comments: 0
Question Number 83019 Answers: 1 Comments: 1
Question Number 83010 Answers: 0 Comments: 0
Question Number 83009 Answers: 0 Comments: 1
Question Number 83008 Answers: 0 Comments: 0
Question Number 82995 Answers: 1 Comments: 1

Question Number 82993 Answers: 1 Comments: 0

Pg 1315 Pg 1316 Pg 1317 Pg 1318 Pg 1319 Pg 1320 Pg 1321 Pg 1322 Pg 1323 Pg 1324
