
AllQuestion and Answers: Page 1317
Question Number 83369 Answers: 1 Comments: 2

Question Number 83367 Answers: 0 Comments: 1
$$\int_{−\infty} ^{\infty} \frac{{sin}^{\mathrm{7}} \left({x}\right)}{{x}^{\mathrm{7}} }{dx} \\ $$
Question Number 83361 Answers: 1 Comments: 1
Question Number 83354 Answers: 0 Comments: 2

Question Number 83352 Answers: 1 Comments: 6
Question Number 83342 Answers: 1 Comments: 0
Question Number 83341 Answers: 1 Comments: 1
Question Number 83340 Answers: 0 Comments: 0
Question Number 83338 Answers: 1 Comments: 0
Question Number 83331 Answers: 1 Comments: 7

Question Number 83329 Answers: 1 Comments: 1
Question Number 83327 Answers: 0 Comments: 2
Question Number 83323 Answers: 1 Comments: 1
Question Number 83319 Answers: 1 Comments: 0
Question Number 83318 Answers: 0 Comments: 0
$${Evaluate} \\ $$$$\int{x}^{\frac{\mathrm{1}}{{x}^{{n}} }} \:{dx}\:,{n}>\mathrm{0} \\ $$
Question Number 83307 Answers: 0 Comments: 4
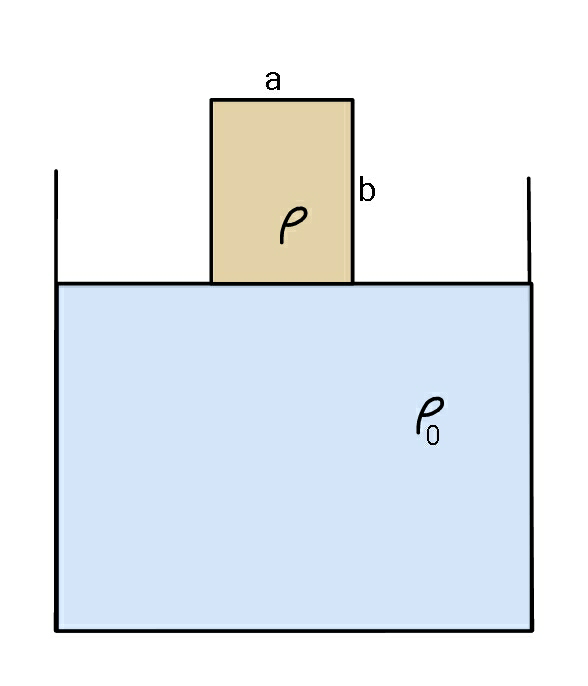
Question Number 83297 Answers: 1 Comments: 1
Question Number 83296 Answers: 0 Comments: 2
Question Number 83295 Answers: 0 Comments: 0
Question Number 83293 Answers: 0 Comments: 0
Question Number 83289 Answers: 3 Comments: 0
Question Number 83288 Answers: 0 Comments: 0

Question Number 83287 Answers: 1 Comments: 0

Question Number 83285 Answers: 1 Comments: 1
Question Number 83276 Answers: 1 Comments: 0
Question Number 83268 Answers: 1 Comments: 0

Pg 1312 Pg 1313 Pg 1314 Pg 1315 Pg 1316 Pg 1317 Pg 1318 Pg 1319 Pg 1320 Pg 1321
