
AllQuestion and Answers: Page 1315
Question Number 83591 Answers: 0 Comments: 1
Question Number 83590 Answers: 0 Comments: 3
Question Number 83587 Answers: 0 Comments: 2
Question Number 83582 Answers: 0 Comments: 0
Question Number 83570 Answers: 2 Comments: 3
Question Number 83569 Answers: 0 Comments: 1
Question Number 83565 Answers: 1 Comments: 4

Question Number 83559 Answers: 1 Comments: 1

Question Number 83558 Answers: 0 Comments: 4

Question Number 83556 Answers: 2 Comments: 0
Question Number 83554 Answers: 1 Comments: 0

Question Number 83543 Answers: 1 Comments: 2

Question Number 83542 Answers: 2 Comments: 0
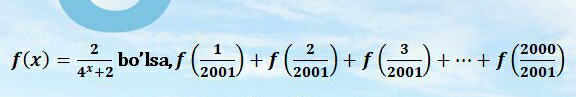
Question Number 83539 Answers: 0 Comments: 3
Question Number 83621 Answers: 2 Comments: 1
Question Number 83524 Answers: 2 Comments: 2

Question Number 83521 Answers: 0 Comments: 1
Question Number 83520 Answers: 1 Comments: 0
Question Number 83513 Answers: 0 Comments: 2
Question Number 83512 Answers: 1 Comments: 0
Question Number 83511 Answers: 1 Comments: 0
Question Number 83500 Answers: 1 Comments: 0
$$\frac{{d}}{{dx}}\left(\left({a}+{bx}\right)^{{c}+{dx}} \right) \\ $$
Question Number 83495 Answers: 0 Comments: 5
Question Number 83493 Answers: 0 Comments: 0
Question Number 83488 Answers: 1 Comments: 0
Question Number 83481 Answers: 1 Comments: 3

Pg 1310 Pg 1311 Pg 1312 Pg 1313 Pg 1314 Pg 1315 Pg 1316 Pg 1317 Pg 1318 Pg 1319
