Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1311

Question Number 83296 Answers: 0 Comments: 2

Obtain a maclaurin expansion for a) e^(cos x ) b) e^(cos^2 x)

$$\mathrm{Obtain}\:\mathrm{a}\:\mathrm{maclaurin}\:\mathrm{expansion}\:\mathrm{for}\: \\ $$$$\left.\mathrm{a}\left.\right)\:\mathrm{e}^{\mathrm{cos}\:{x}\:} \:\:\:\:\:\:\:\:\mathrm{b}\right)\:\mathrm{e}^{\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$

Question Number 83295 Answers: 0 Comments: 0

Expand ln (1 + sinh x) as a series in ascending powers of x up to and including the term in x^3 . Hence , show that (1 + sinh x)^(3/x) ≅ e^2 (1 −x + (x^2 /2))

$$\mathrm{Expand}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{sinh}\:{x}\right)\:\mathrm{as}\:\mathrm{a}\:\mathrm{series}\:\mathrm{in} \\ $$$$\mathrm{ascending}\:\mathrm{powers}\:\mathrm{of}\:{x}\:\mathrm{up}\:\mathrm{to}\:\mathrm{and}\:\mathrm{including} \\ $$$$\mathrm{the}\:\mathrm{term}\:\mathrm{in}\:{x}^{\mathrm{3}} \:.\:\mathrm{Hence}\:,\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\:\left(\mathrm{1}\:+\:\mathrm{sinh}\:{x}\right)^{\frac{\mathrm{3}}{{x}}} \:\cong\:{e}^{\mathrm{2}} \left(\mathrm{1}\:−{x}\:+\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$

Question Number 83293 Answers: 0 Comments: 0

Let A (((−2)),((−1)) ) ,B ((1),(3) ) , C (((−10)),(( 5)) ) three given points in the brand (O,I,J) such as OI=OJ and (OI)⊥(OJ) D is a point such as AD=AC+2 and CD=2 Prove correctly that BD=13 .Can you find the coordinate of D?

$${Let}\:\:{A}\begin{pmatrix}{−\mathrm{2}}\\{−\mathrm{1}}\end{pmatrix}\:\:,{B}\begin{pmatrix}{\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:,\:{C}\begin{pmatrix}{−\mathrm{10}}\\{\:\mathrm{5}}\end{pmatrix}\:{three}\:{given}\:{points}\:{in}\:{the}\:{brand}\:\left({O},{I},{J}\right)\:{such}\:{as}\:{OI}={OJ}\:{and}\:\left({OI}\right)\bot\left({OJ}\right) \\ $$$$\:{D}\:{is}\:{a}\:{point}\:{such}\:{as}\:{AD}={AC}+\mathrm{2}\:\:{and}\:\:{CD}=\mathrm{2}\: \\ $$$${Prove}\:{correctly}\:{that}\:\:{BD}=\mathrm{13}\:.{Can}\:{you}\:{find}\:{the}\:{coordinate}\:{of}\:{D}? \\ $$

Question Number 83289 Answers: 3 Comments: 0

solve log_((24sinx)) (24cosx)=(3/2)

$$\:\:{solve} \\ $$$$\boldsymbol{{log}}_{\left(\mathrm{24}\boldsymbol{{sinx}}\right)} \left(\mathrm{24}\boldsymbol{{cosx}}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Question Number 83288 Answers: 0 Comments: 0

Question Number 83287 Answers: 1 Comments: 0

Question Number 83285 Answers: 1 Comments: 1

3^((x+2)(x−4)) ≤ 7^(x+2) find solution

$$\mathrm{3}^{\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}−\mathrm{4}\right)} \:\leqslant\:\mathrm{7}^{\mathrm{x}+\mathrm{2}} \\ $$$$\mathrm{find}\:\mathrm{solution} \\ $$

Question Number 83276 Answers: 1 Comments: 0

∫sec^5 3x•sec3xtan 3xdx

$$\int\mathrm{s}{ec}^{\mathrm{5}} \mathrm{3}{x}\bullet\mathrm{s}{ec}\mathrm{3}{x}\mathrm{tan}\:\mathrm{3}{xdx} \\ $$

Question Number 83268 Answers: 1 Comments: 0

Question Number 83266 Answers: 1 Comments: 1

∫sin^(10) Θcos ΘdΘ

$$\int\mathrm{sin}^{\mathrm{10}} \Theta\mathrm{cos}\:\Theta{d}\Theta\: \\ $$

Question Number 83264 Answers: 1 Comments: 2

Question Number 83262 Answers: 1 Comments: 0

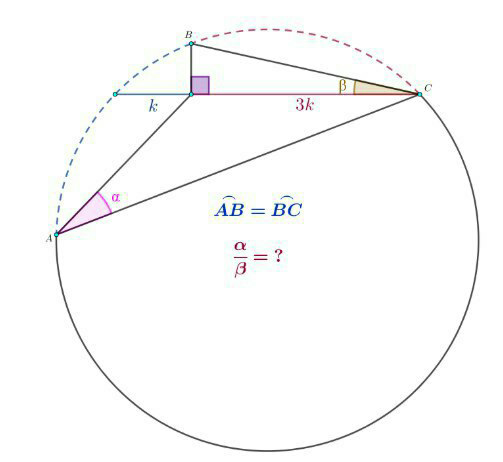
Question Number 83261 Answers: 0 Comments: 1

Question Number 83259 Answers: 1 Comments: 0

∫x^9 sin x^(10) dx

$$\int{x}^{\mathrm{9}} \mathrm{sin}\:{x}^{\mathrm{10}} {dx} \\ $$

Question Number 83257 Answers: 1 Comments: 0

find the derivtive of y=((10^x )/(log_(10) x))

$${find}\:{the}\:{derivtive}\:{of}\:{y}=\frac{\mathrm{10}^{{x}} }{{log}_{\mathrm{10}} {x}} \\ $$

Question Number 83255 Answers: 0 Comments: 0

let g(x)=ln(2−cosx) devlopp g at integr serie

$${let}\:{g}\left({x}\right)={ln}\left(\mathrm{2}−{cosx}\right) \\ $$$${devlopp}\:{g}\:{at}\:{integr}\:{serie} \\ $$

Question Number 83254 Answers: 0 Comments: 1

let f(x)=arctan(2x−(1/x)) find f^((n)) (x) andf^((n)) (1)

$${let}\:{f}\left({x}\right)={arctan}\left(\mathrm{2}{x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${find}\:{f}^{\left({n}\right)} \left({x}\right)\:{andf}^{\left({n}\right)} \left(\mathrm{1}\right) \\ $$

Question Number 83253 Answers: 0 Comments: 3

calculate ∫_0 ^∞ (dx/((x^4 −x^2 +1)^2 ))

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 83252 Answers: 1 Comments: 1

calculate ∫_0 ^(π/2) (dx/(cos^2 x +(√3)sin^2 x))

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{{cos}^{\mathrm{2}} {x}\:+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} {x}} \\ $$

Question Number 83251 Answers: 0 Comments: 1

calculate ∫ ch^2 (x)sin^3 xdx

$${calculate}\:\:\int\:\:{ch}^{\mathrm{2}} \left({x}\right){sin}^{\mathrm{3}} \:{xdx} \\ $$

Question Number 83250 Answers: 1 Comments: 0

1)decompose F(x)=((x^2 −3)/(2x^3 +5x+7)) 2)determine ∫ F(x)dx

$$\left.\mathrm{1}\right){decompose}\:{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{2}{x}^{\mathrm{3}} \:+\mathrm{5}{x}+\mathrm{7}} \\ $$$$\left.\mathrm{2}\right){determine}\:\int\:{F}\left({x}\right){dx} \\ $$

Question Number 83246 Answers: 0 Comments: 0

fnd ∫ xe^(−x^2 ) arctan(1−(1/x))dx

$${fnd}\:\int\:{xe}^{−{x}^{\mathrm{2}} } {arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$

Question Number 83245 Answers: 0 Comments: 2

let f(x) =e^(−2x) ln(1+2x) 1) find f^((n)) (x) and f^((n)) (0) 2)developp f at integr serie

$${let}\:{f}\left({x}\right)\:={e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$

Question Number 83242 Answers: 0 Comments: 3

Question Number 83240 Answers: 0 Comments: 1

Question Number 83235 Answers: 0 Comments: 2

Pg 1306 Pg 1307 Pg 1308 Pg 1309 Pg 1310 Pg 1311 Pg 1312 Pg 1313 Pg 1314 Pg 1315

Terms of Service

Contact: info@tinkutara.com