Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1305

Question Number 83268 Answers: 1 Comments: 0

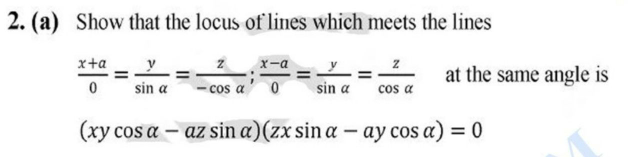
Question Number 83266 Answers: 1 Comments: 1

∫sin^(10) Θcos ΘdΘ

$$\int\mathrm{sin}^{\mathrm{10}} \Theta\mathrm{cos}\:\Theta{d}\Theta\: \\ $$

Question Number 83264 Answers: 1 Comments: 2

Question Number 83262 Answers: 1 Comments: 0

Question Number 83261 Answers: 0 Comments: 1

Question Number 83259 Answers: 1 Comments: 0

∫x^9 sin x^(10) dx

$$\int{x}^{\mathrm{9}} \mathrm{sin}\:{x}^{\mathrm{10}} {dx} \\ $$

Question Number 83257 Answers: 1 Comments: 0

find the derivtive of y=((10^x )/(log_(10) x))

$${find}\:{the}\:{derivtive}\:{of}\:{y}=\frac{\mathrm{10}^{{x}} }{{log}_{\mathrm{10}} {x}} \\ $$

Question Number 83255 Answers: 0 Comments: 0

let g(x)=ln(2−cosx) devlopp g at integr serie

$${let}\:{g}\left({x}\right)={ln}\left(\mathrm{2}−{cosx}\right) \\ $$$${devlopp}\:{g}\:{at}\:{integr}\:{serie} \\ $$

Question Number 83254 Answers: 0 Comments: 1

let f(x)=arctan(2x−(1/x)) find f^((n)) (x) andf^((n)) (1)

$${let}\:{f}\left({x}\right)={arctan}\left(\mathrm{2}{x}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${find}\:{f}^{\left({n}\right)} \left({x}\right)\:{andf}^{\left({n}\right)} \left(\mathrm{1}\right) \\ $$

Question Number 83253 Answers: 0 Comments: 3

calculate ∫_0 ^∞ (dx/((x^4 −x^2 +1)^2 ))

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 83252 Answers: 1 Comments: 1

calculate ∫_0 ^(π/2) (dx/(cos^2 x +(√3)sin^2 x))

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{{cos}^{\mathrm{2}} {x}\:+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} {x}} \\ $$

Question Number 83251 Answers: 0 Comments: 1

calculate ∫ ch^2 (x)sin^3 xdx

$${calculate}\:\:\int\:\:{ch}^{\mathrm{2}} \left({x}\right){sin}^{\mathrm{3}} \:{xdx} \\ $$

Question Number 83250 Answers: 1 Comments: 0

1)decompose F(x)=((x^2 −3)/(2x^3 +5x+7)) 2)determine ∫ F(x)dx

$$\left.\mathrm{1}\right){decompose}\:{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{2}{x}^{\mathrm{3}} \:+\mathrm{5}{x}+\mathrm{7}} \\ $$$$\left.\mathrm{2}\right){determine}\:\int\:{F}\left({x}\right){dx} \\ $$

Question Number 83246 Answers: 0 Comments: 0

fnd ∫ xe^(−x^2 ) arctan(1−(1/x))dx

$${fnd}\:\int\:{xe}^{−{x}^{\mathrm{2}} } {arctan}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$

Question Number 83245 Answers: 0 Comments: 2

let f(x) =e^(−2x) ln(1+2x) 1) find f^((n)) (x) and f^((n)) (0) 2)developp f at integr serie

$${let}\:{f}\left({x}\right)\:={e}^{−\mathrm{2}{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}^{\left({n}\right)} \left({x}\right)\:{and}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$

Question Number 83242 Answers: 0 Comments: 3

Question Number 83240 Answers: 0 Comments: 1

Question Number 83235 Answers: 0 Comments: 2

Question Number 83229 Answers: 0 Comments: 4

Question Number 83226 Answers: 1 Comments: 1

∫_( 0) ^1 (1/(x^2 +2x cos α+1)) dx =

$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}{x}\:\mathrm{cos}\:\alpha+\mathrm{1}}\:{dx}\:= \\ $$

Question Number 83225 Answers: 0 Comments: 1

∫_( 0) ^(100) sin (x−[x])π dx =

$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{100}} {\int}}\:\mathrm{sin}\:\left({x}−\left[{x}\right]\right)\pi\:{dx}\:= \\ $$

Question Number 83214 Answers: 1 Comments: 0

calculate U_n =Σ_(k=0) ^n (1/(3k+1)) interms of H_n =Σ_(k=1) ^n (1/k)

$${calculate}\:\:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:{interms}\:{of}\:{H}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$

Question Number 83213 Answers: 0 Comments: 0

Prove that ∀ θ∈R Σ_(n=1) ^∞ 3^(n−1) sin^3 ((θ/3^n ))= ((θ−sinθ)/4)

$${Prove}\:\:{that}\:\:\forall\:\theta\in\mathbb{R}\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{3}^{{n}−\mathrm{1}} {sin}^{\mathrm{3}} \left(\frac{\theta}{\mathrm{3}^{{n}} }\right)=\:\frac{\theta−{sin}\theta}{\mathrm{4}}\: \\ $$

Question Number 83209 Answers: 1 Comments: 0

Prove that ∀ x≠(π/4) , Π_(n=0) ^∞ (((cos((x/2^n ))+cos(((π−2x)/2^(n+1) )))/2) ) = ((4cos2x)/(π(π−4x)))

$$\:\:\:{Prove}\:{that}\:\:\forall\:\:{x}\neq\frac{\pi}{\mathrm{4}}\:\:\:,\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\prod}}\left(\frac{{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)+{cos}\left(\frac{\pi−\mathrm{2}{x}}{\mathrm{2}^{{n}+\mathrm{1}} }\right)}{\mathrm{2}}\:\right)\:=\:\frac{\mathrm{4}{cos}\mathrm{2}{x}}{\pi\left(\pi−\mathrm{4}{x}\right)}\: \\ $$

Question Number 83206 Answers: 0 Comments: 2

1) find ∫_0 ^(π/4) (dx/(2+a sinx)) (areal) 2) c explicite ∫_0 ^(π/4) ((sinx)/((2+asinx)^2 ))dx

$$\left.\mathrm{1}\right)\:{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{dx}}{\mathrm{2}+{a}\:{sinx}}\:\:\:\:\left({areal}\right) \\ $$$$\left.\mathrm{2}\right)\:{c}\:{explicite}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{sinx}}{\left(\mathrm{2}+{asinx}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 83205 Answers: 0 Comments: 2

∫_0 ^(ln2) (1/(cosh(x + ln4)))dx =

$$\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{\mathrm{1}}{{cosh}\left({x}\:+\:{ln}\mathrm{4}\right)}{dx}\:= \\ $$

Pg 1300 Pg 1301 Pg 1302 Pg 1303 Pg 1304 Pg 1305 Pg 1306 Pg 1307 Pg 1308 Pg 1309

Contact: info@tinkutara.com