
AllQuestion and Answers: Page 1275
Question Number 88212 Answers: 0 Comments: 0
Question Number 88211 Answers: 0 Comments: 0

Question Number 88210 Answers: 1 Comments: 0
Question Number 88207 Answers: 1 Comments: 1
Question Number 88206 Answers: 1 Comments: 0
Question Number 88204 Answers: 0 Comments: 0
Question Number 88203 Answers: 0 Comments: 0
Question Number 88198 Answers: 1 Comments: 0
Question Number 88197 Answers: 0 Comments: 0
Question Number 88196 Answers: 0 Comments: 0

Question Number 88194 Answers: 0 Comments: 4
Question Number 88188 Answers: 1 Comments: 5

Question Number 88181 Answers: 0 Comments: 1

Question Number 88180 Answers: 0 Comments: 0
$$\left(\mathrm{5}+\mathrm{4}{y}\right)×{dy}={y}^{\mathrm{3}} {x}\: \\ $$
Question Number 88179 Answers: 1 Comments: 0
$${z}={x}^{\mathrm{2}} /{y}^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\:{dz}=? \\ $$
Question Number 88178 Answers: 0 Comments: 0
Question Number 88177 Answers: 1 Comments: 0
Question Number 88170 Answers: 0 Comments: 2
Question Number 88169 Answers: 1 Comments: 2
Question Number 88160 Answers: 2 Comments: 1
Question Number 88153 Answers: 0 Comments: 1
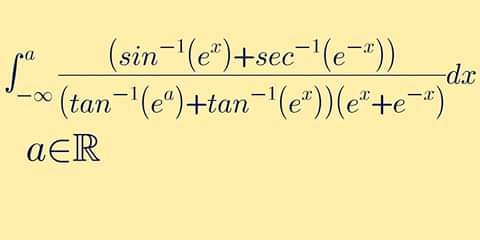
Question Number 88141 Answers: 1 Comments: 0

Question Number 88137 Answers: 1 Comments: 2
Question Number 88131 Answers: 1 Comments: 0
$$\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}−\sqrt{\mathrm{1}−\mathrm{2}{x}}}{dx} \\ $$
Question Number 91093 Answers: 0 Comments: 16
Question Number 88128 Answers: 1 Comments: 0
Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274 Pg 1275 Pg 1276 Pg 1277 Pg 1278 Pg 1279
