
AllQuestion and Answers: Page 1274
Question Number 88300 Answers: 0 Comments: 0
Question Number 88307 Answers: 1 Comments: 0
Question Number 88289 Answers: 0 Comments: 5

Question Number 88288 Answers: 1 Comments: 1
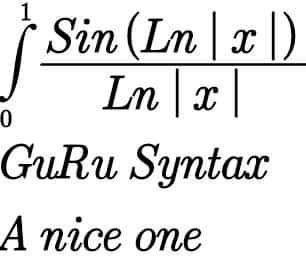
Question Number 88286 Answers: 0 Comments: 1

Question Number 88272 Answers: 1 Comments: 1
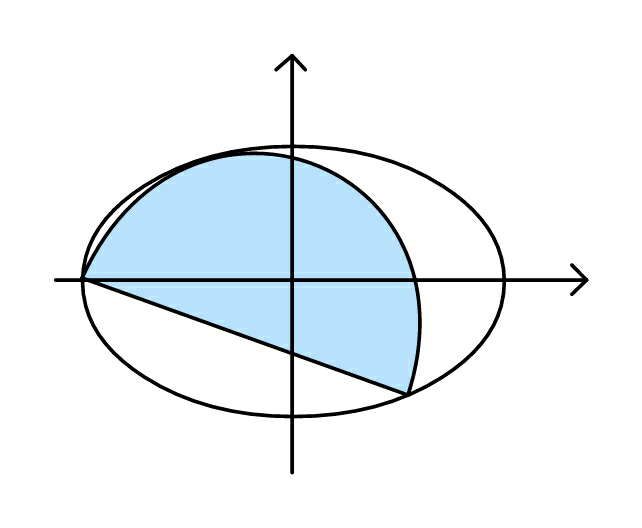
Question Number 88270 Answers: 0 Comments: 1
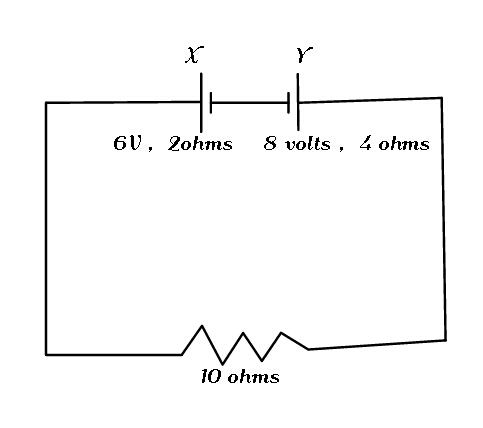
Question Number 88263 Answers: 1 Comments: 1
Question Number 88261 Answers: 1 Comments: 0

Question Number 88253 Answers: 0 Comments: 0
$$\int\:\frac{\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:{dx}}{{x}+\mathrm{1}}\: \\ $$
Question Number 88252 Answers: 0 Comments: 0

Question Number 88251 Answers: 0 Comments: 0

Question Number 88245 Answers: 2 Comments: 0

Question Number 88240 Answers: 1 Comments: 3

Question Number 88239 Answers: 0 Comments: 0
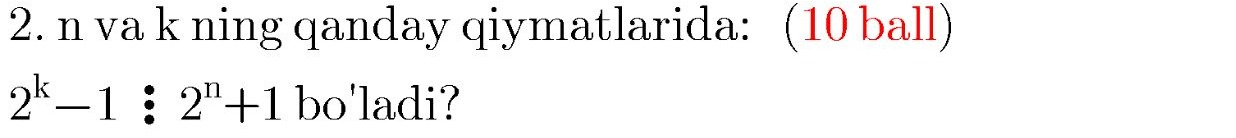
Question Number 88238 Answers: 1 Comments: 0
Question Number 88236 Answers: 1 Comments: 0
Question Number 88235 Answers: 0 Comments: 1
Question Number 88232 Answers: 0 Comments: 0
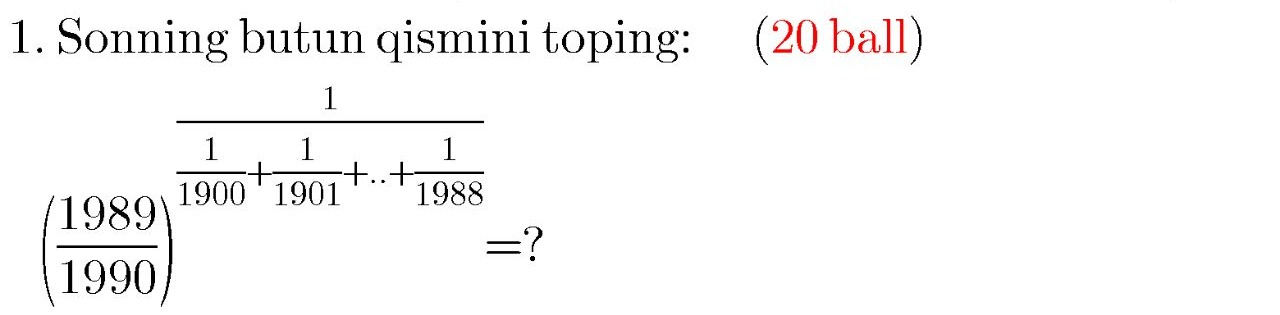
Question Number 88218 Answers: 1 Comments: 2

Question Number 88214 Answers: 2 Comments: 0

Question Number 88212 Answers: 0 Comments: 0
Question Number 88211 Answers: 0 Comments: 0

Question Number 88210 Answers: 1 Comments: 0
Question Number 88207 Answers: 1 Comments: 1
Question Number 88206 Answers: 1 Comments: 0
Pg 1269 Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274 Pg 1275 Pg 1276 Pg 1277 Pg 1278
