
AllQuestion and Answers: Page 1273
Question Number 88439 Answers: 0 Comments: 4
Question Number 88438 Answers: 2 Comments: 0
$$\int\frac{{x}^{\mathrm{5}} +\mathrm{1}}{{x}^{\mathrm{5}} −\mathrm{1}}{dx} \\ $$
Question Number 88436 Answers: 0 Comments: 0
Question Number 88435 Answers: 0 Comments: 0
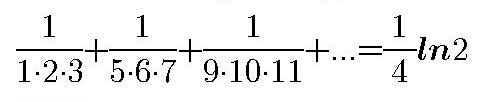
Question Number 88434 Answers: 0 Comments: 2
Question Number 88430 Answers: 1 Comments: 1
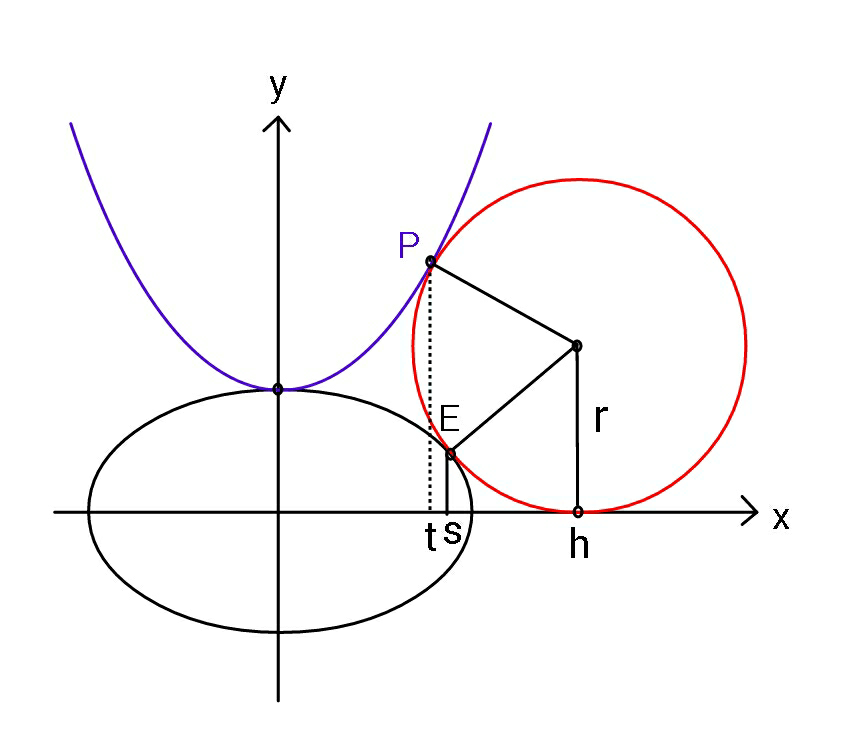
Question Number 88429 Answers: 0 Comments: 0
Question Number 88424 Answers: 0 Comments: 1
Question Number 88423 Answers: 0 Comments: 1
Question Number 88422 Answers: 0 Comments: 1
Question Number 88419 Answers: 0 Comments: 0
Question Number 88417 Answers: 0 Comments: 1
Question Number 88415 Answers: 0 Comments: 2
Question Number 88414 Answers: 0 Comments: 2
Question Number 88413 Answers: 0 Comments: 3
$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$ \\ $$
Question Number 88388 Answers: 1 Comments: 0
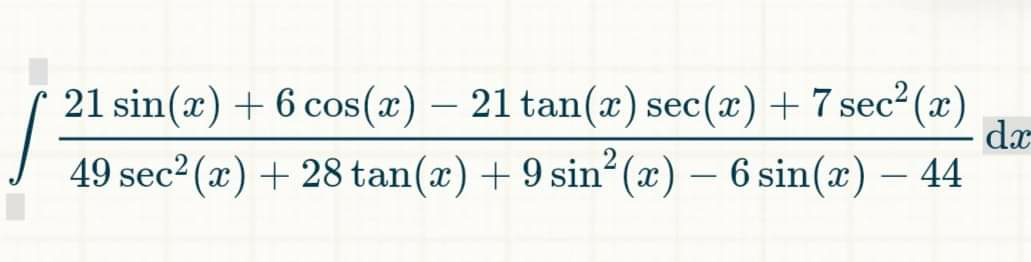
Question Number 88385 Answers: 0 Comments: 0
Question Number 88378 Answers: 1 Comments: 4
Question Number 88372 Answers: 0 Comments: 10
Question Number 88364 Answers: 1 Comments: 0

Question Number 88360 Answers: 0 Comments: 2
Question Number 88357 Answers: 0 Comments: 1
Question Number 88352 Answers: 1 Comments: 1
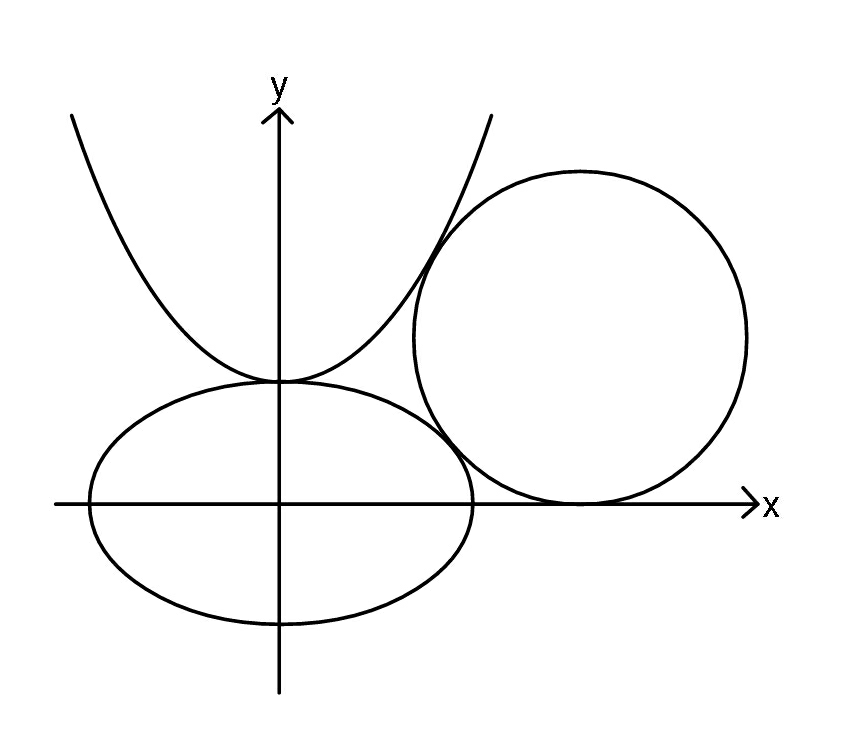
Question Number 88349 Answers: 1 Comments: 1
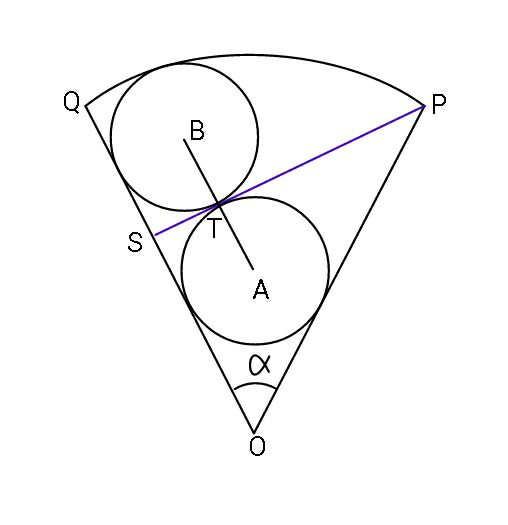
Question Number 88339 Answers: 3 Comments: 3
$$\:\int\left(\:\sqrt{\mathrm{tan}\:{x}\:}\:+\:\sqrt{\mathrm{cot}\:{x}}\:\right){dx}\:=\:? \\ $$
Question Number 88329 Answers: 0 Comments: 4

Pg 1268 Pg 1269 Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274 Pg 1275 Pg 1276 Pg 1277
