
AllQuestion and Answers: Page 1272
Question Number 88586 Answers: 1 Comments: 0
$$\int\frac{\sqrt{{cos}\left(\mathrm{2}{x}\right)+\mathrm{3}}}{{cos}\left({x}\right)}{dx} \\ $$
Question Number 88590 Answers: 0 Comments: 0
$${a}^{{a}^{{a}^{{a}^{\mathrm{3}} } } } =\mathrm{5} \\ $$$${find}−{a} \\ $$
Question Number 88580 Answers: 0 Comments: 4
Question Number 88569 Answers: 1 Comments: 1

Question Number 88567 Answers: 0 Comments: 1
Question Number 88559 Answers: 0 Comments: 1
Question Number 88555 Answers: 1 Comments: 0
Question Number 88552 Answers: 0 Comments: 0
Question Number 88547 Answers: 1 Comments: 0
Question Number 88541 Answers: 1 Comments: 5
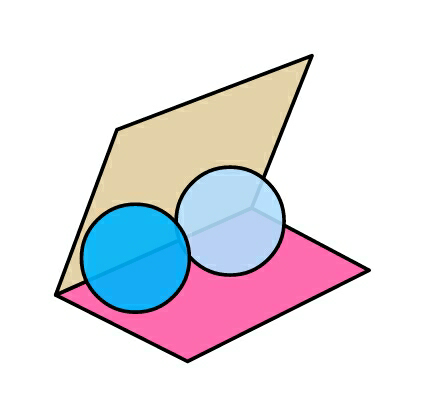
Question Number 88525 Answers: 1 Comments: 6

Question Number 88507 Answers: 1 Comments: 1
Question Number 88503 Answers: 0 Comments: 3
Question Number 88494 Answers: 0 Comments: 2
$$\int\:\sqrt{\mathrm{cos}\left(\mathrm{x}\right)}\:\:\mathrm{dx} \\ $$
Question Number 88492 Answers: 0 Comments: 4
Question Number 88491 Answers: 1 Comments: 0
$$\boldsymbol{{solve}} \\ $$$${cos}\left({x}\right)={k} \\ $$
Question Number 88490 Answers: 0 Comments: 4
$$\int_{\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{4}} }{\mathrm{4}^{{x}} }{dx}=? \\ $$
Question Number 88487 Answers: 0 Comments: 7
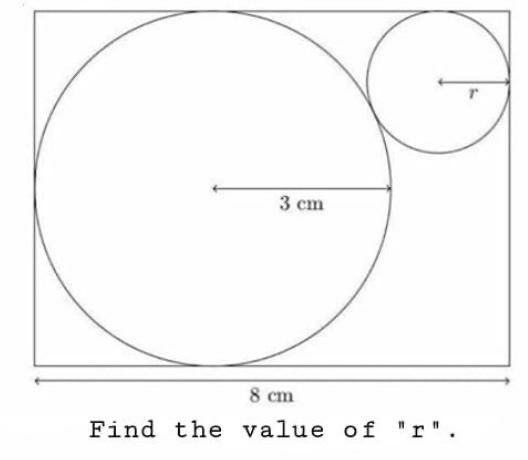
Question Number 88479 Answers: 0 Comments: 0
Question Number 88473 Answers: 0 Comments: 2

Question Number 88471 Answers: 1 Comments: 0

Question Number 88461 Answers: 0 Comments: 2

Question Number 88458 Answers: 0 Comments: 0
Question Number 88456 Answers: 1 Comments: 4
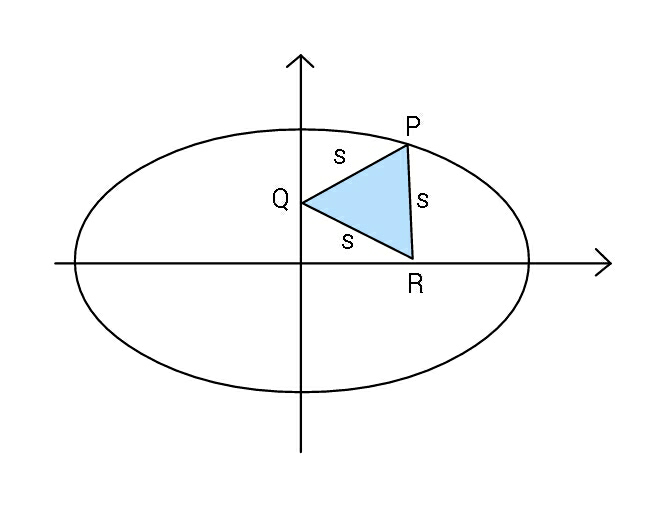
Question Number 88462 Answers: 0 Comments: 3

Question Number 88440 Answers: 2 Comments: 2
Pg 1267 Pg 1268 Pg 1269 Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274 Pg 1275 Pg 1276
