
AllQuestion and Answers: Page 1271
Question Number 88756 Answers: 0 Comments: 0
Question Number 88754 Answers: 1 Comments: 3
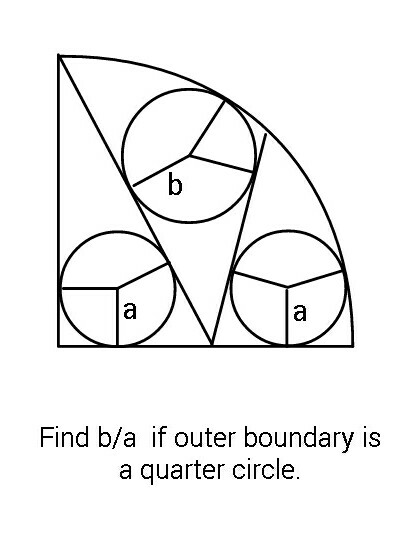
Question Number 88752 Answers: 1 Comments: 2
Question Number 88731 Answers: 0 Comments: 3

Question Number 88723 Answers: 1 Comments: 0
Question Number 88710 Answers: 2 Comments: 1
Question Number 88708 Answers: 2 Comments: 5

Question Number 88690 Answers: 1 Comments: 0

Question Number 88683 Answers: 2 Comments: 0

Question Number 88681 Answers: 0 Comments: 2
Question Number 88678 Answers: 0 Comments: 8
$$\boldsymbol{\mathrm{F}}{ind}\:\:\:\sqrt{\boldsymbol{{i}}}+\sqrt{−\boldsymbol{\mathrm{i}}} \\ $$
Question Number 88673 Answers: 2 Comments: 2
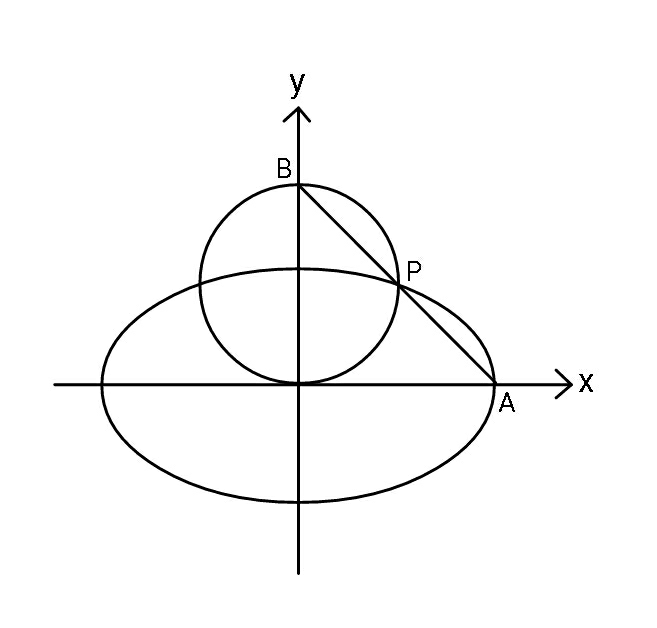
Question Number 88663 Answers: 1 Comments: 0
Question Number 88656 Answers: 1 Comments: 1
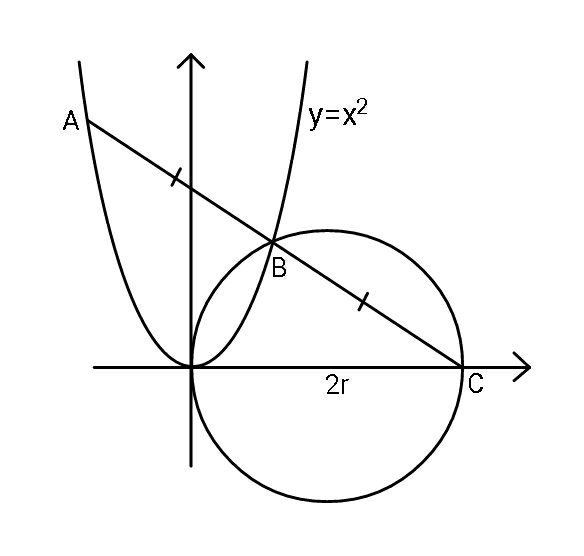
Question Number 88642 Answers: 1 Comments: 2

Question Number 88623 Answers: 2 Comments: 4

Question Number 88616 Answers: 1 Comments: 9

Question Number 88613 Answers: 1 Comments: 3

Question Number 88611 Answers: 0 Comments: 0
Question Number 88610 Answers: 0 Comments: 2
Question Number 88607 Answers: 0 Comments: 0
Question Number 88606 Answers: 2 Comments: 2

Question Number 88603 Answers: 1 Comments: 0

Question Number 88594 Answers: 0 Comments: 3
$${solve}\:{for}\:{x}\in\mathbb{C} \\ $$$$\mathrm{cos}\:\left({x}\right)={a}+{bi} \\ $$
Question Number 88592 Answers: 1 Comments: 0
Question Number 88586 Answers: 1 Comments: 0
$$\int\frac{\sqrt{{cos}\left(\mathrm{2}{x}\right)+\mathrm{3}}}{{cos}\left({x}\right)}{dx} \\ $$
Pg 1266 Pg 1267 Pg 1268 Pg 1269 Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274 Pg 1275
