
AllQuestion and Answers: Page 1270
Question Number 88892 Answers: 0 Comments: 2

Question Number 88894 Answers: 0 Comments: 1
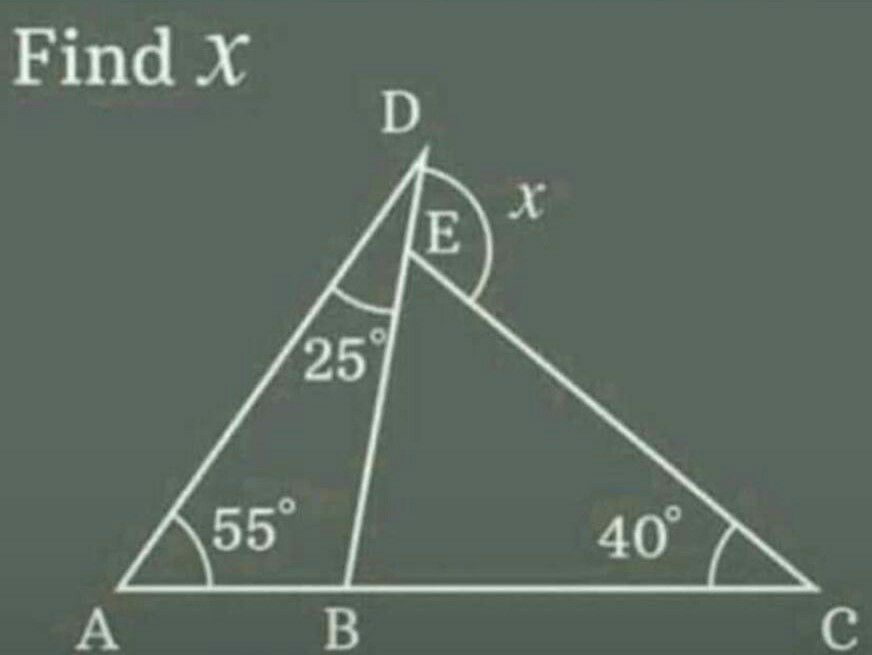
Question Number 88889 Answers: 0 Comments: 1

Question Number 88886 Answers: 1 Comments: 5

Question Number 88882 Answers: 1 Comments: 1
Question Number 88881 Answers: 1 Comments: 0

Question Number 88876 Answers: 0 Comments: 2
Question Number 88873 Answers: 0 Comments: 1
$$\mathrm{3}+\sqrt{{x}^{\mathrm{2}} −\mathrm{5}}\:>\:\mid{x}−\mathrm{1}\mid\: \\ $$
Question Number 88872 Answers: 0 Comments: 1
Question Number 88871 Answers: 0 Comments: 0

Question Number 88867 Answers: 1 Comments: 1

Question Number 88865 Answers: 0 Comments: 1

Question Number 88863 Answers: 0 Comments: 1
Question Number 88860 Answers: 0 Comments: 3

Question Number 88859 Answers: 0 Comments: 1
Question Number 88858 Answers: 0 Comments: 0
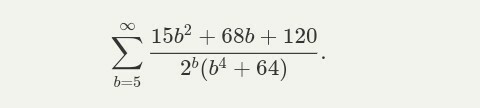
Question Number 88852 Answers: 1 Comments: 0
Question Number 88851 Answers: 0 Comments: 1
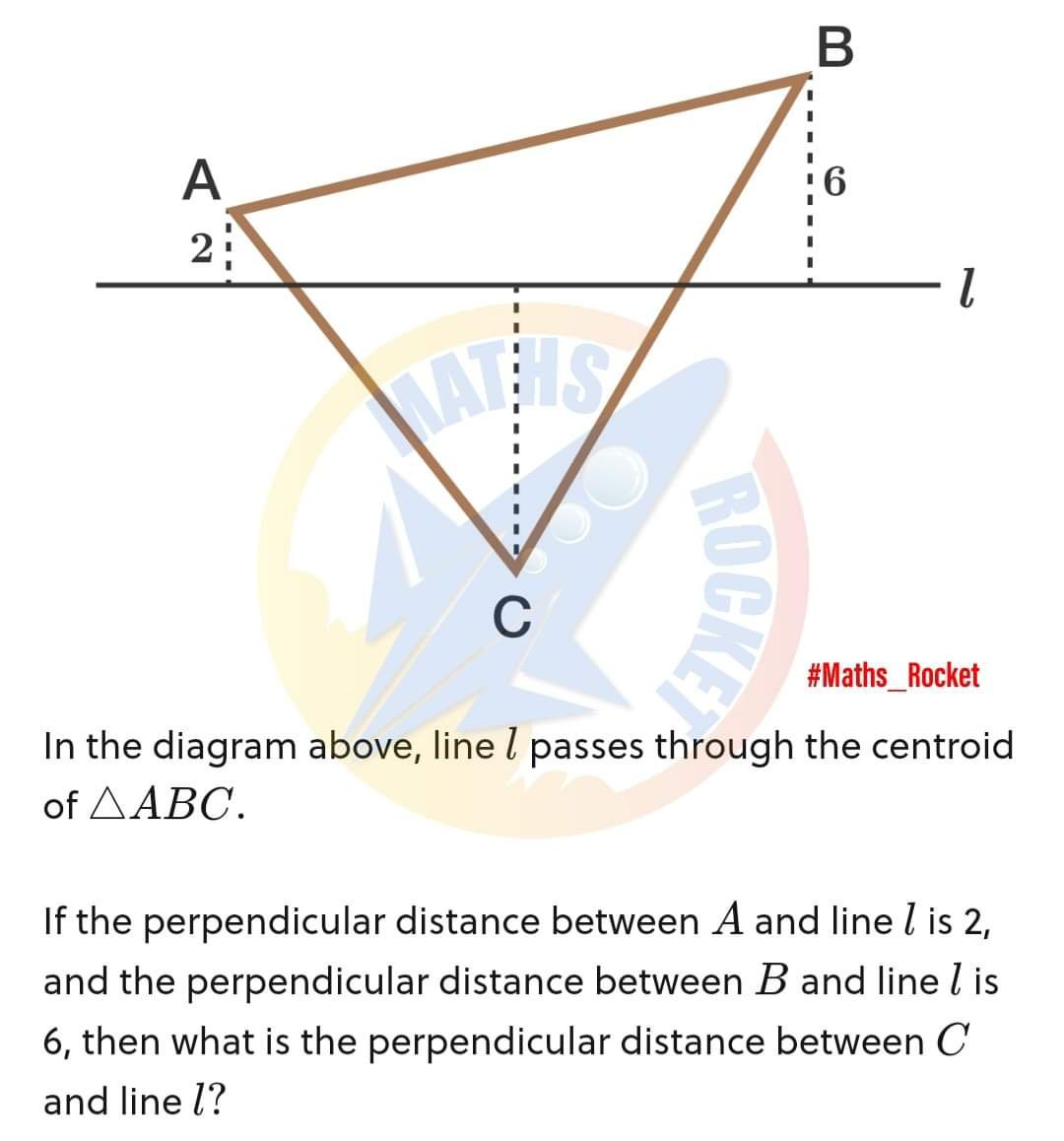
Question Number 88820 Answers: 2 Comments: 5

Question Number 88811 Answers: 1 Comments: 0
Question Number 88789 Answers: 0 Comments: 7
Question Number 88778 Answers: 0 Comments: 3

Question Number 88794 Answers: 1 Comments: 0
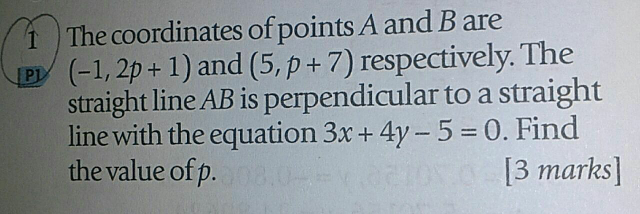
Question Number 88771 Answers: 0 Comments: 4
Question Number 88761 Answers: 0 Comments: 4
Question Number 88758 Answers: 2 Comments: 22
Pg 1265 Pg 1266 Pg 1267 Pg 1268 Pg 1269 Pg 1270 Pg 1271 Pg 1272 Pg 1273 Pg 1274
