
AllQuestion and Answers: Page 1262
Question Number 89848 Answers: 0 Comments: 1
Question Number 89846 Answers: 1 Comments: 3
Question Number 89835 Answers: 2 Comments: 0
Question Number 89834 Answers: 1 Comments: 1
Question Number 89829 Answers: 0 Comments: 9

Question Number 89826 Answers: 0 Comments: 0
Question Number 89809 Answers: 3 Comments: 0
Question Number 89805 Answers: 1 Comments: 3
Question Number 89804 Answers: 1 Comments: 0
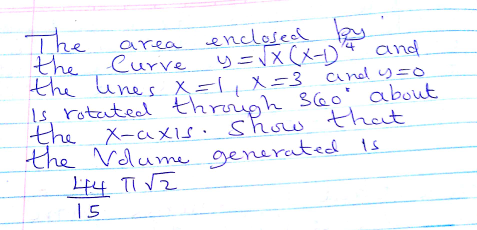
Question Number 89816 Answers: 0 Comments: 3

Question Number 89817 Answers: 0 Comments: 0

Question Number 89795 Answers: 1 Comments: 0

Question Number 89794 Answers: 0 Comments: 1
Question Number 89781 Answers: 0 Comments: 8
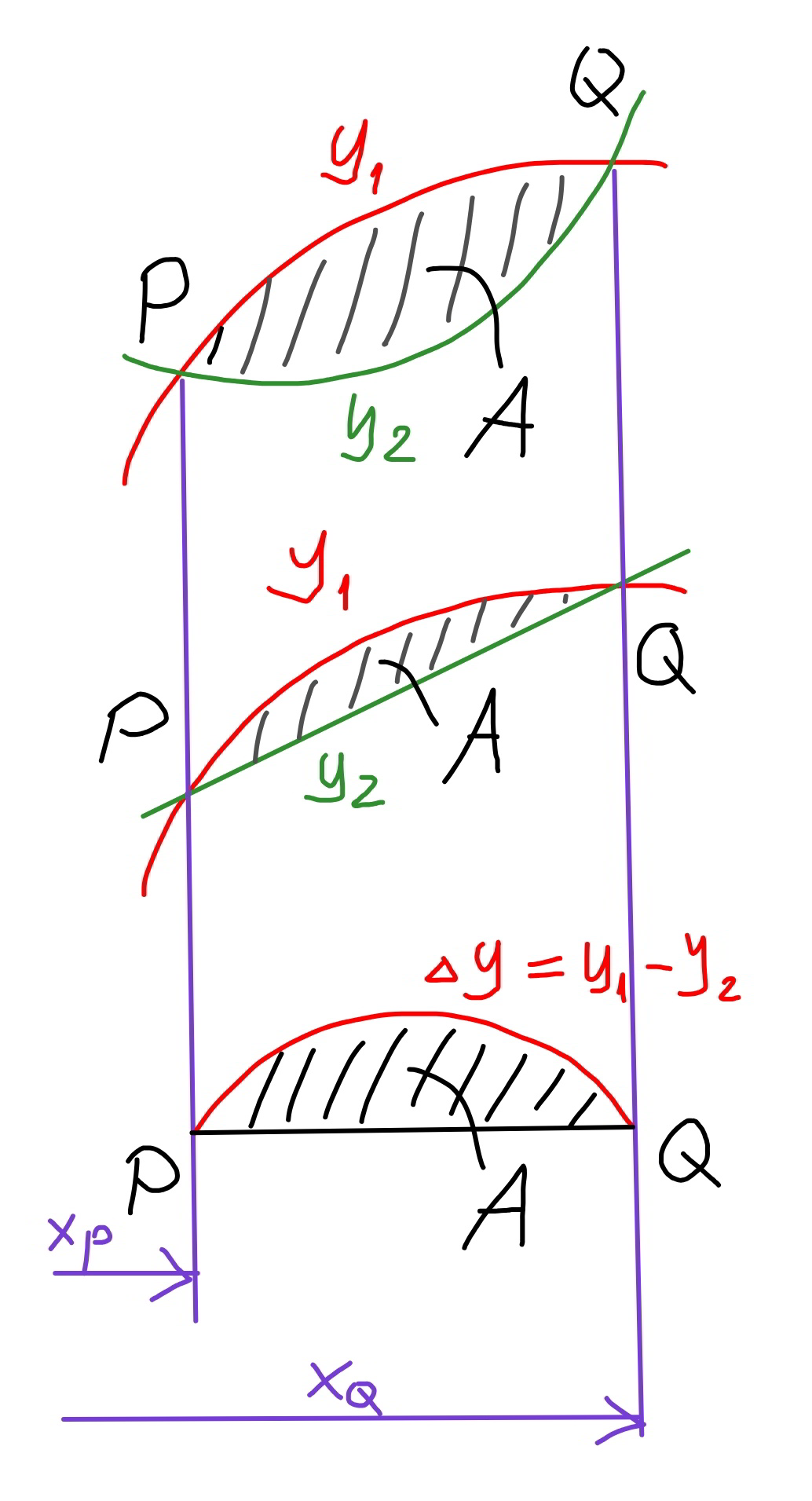
Question Number 89776 Answers: 0 Comments: 2
Question Number 89768 Answers: 2 Comments: 0
Question Number 89755 Answers: 1 Comments: 1

Question Number 89753 Answers: 1 Comments: 6
Question Number 89749 Answers: 0 Comments: 4

Question Number 89748 Answers: 0 Comments: 4
$$\mathrm{dx}\:=\:\left(\mathrm{1}+\mathrm{2xtan}\:\mathrm{y}\right)\:\mathrm{dy}\: \\ $$
Question Number 89745 Answers: 0 Comments: 2
Question Number 89920 Answers: 0 Comments: 1
Question Number 89741 Answers: 0 Comments: 1

Question Number 89737 Answers: 0 Comments: 0

Question Number 89736 Answers: 0 Comments: 1

Question Number 89735 Answers: 0 Comments: 1

Pg 1257 Pg 1258 Pg 1259 Pg 1260 Pg 1261 Pg 1262 Pg 1263 Pg 1264 Pg 1265 Pg 1266
