Question and Answers Forum

AllQuestion and Answers: Page 1261

Question Number 89317 Answers: 1 Comments: 2

find ∫ (dx/((x+(√(x−1)))^2 ))

$${find}\:\int\:\:\:\:\:\frac{{dx}}{\left({x}+\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$

Question Number 89316 Answers: 0 Comments: 0

calculate Σ_(n=2) ^∞ ((2n+1)/((n−1)^3 (n+1)^3 ))

$${calculate}\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\left({n}−\mathrm{1}\right)^{\mathrm{3}} \left({n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Question Number 89315 Answers: 0 Comments: 0

calculate ∫∫_([0,1]^2 ) ((arctan(xy))/((x+y)^2 ))dxdy

$${calculate}\:\int\int_{\left[\mathrm{0},\mathrm{1}\right]^{\mathrm{2}} } \:\:\:\frac{{arctan}\left({xy}\right)}{\left({x}+{y}\right)^{\mathrm{2}} }{dxdy} \\ $$

Question Number 89314 Answers: 0 Comments: 1

calculate ∫∫_D x^2 (√(x+y))dxdy with D is the triangle 0 A B (0 origin) A(1,0) B(0,1)

$${calculate}\:\int\int_{{D}} \:{x}^{\mathrm{2}} \sqrt{{x}+{y}}{dxdy}\:{with}\:{D}\:{is}\:{the}\:{triangle} \\ $$$$\mathrm{0}\:{A}\:{B}\:\:\:\left(\mathrm{0}\:{origin}\right)\:\:\:{A}\left(\mathrm{1},\mathrm{0}\right)\:\:\:{B}\left(\mathrm{0},\mathrm{1}\right) \\ $$

Question Number 89313 Answers: 0 Comments: 1

find the sum Σ_(n=1) ^∞ (1/(n^2 ×3^n ))

$${find}\:{the}\:{sum}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} ×\mathrm{3}^{{n}} } \\ $$

Question Number 89312 Answers: 0 Comments: 1

calculate ∫∫_D xe^(−x) siny dy with D is the triangle OAB O(0,0) A(1,0) B(0,1)

$${calculate}\:\int\int_{{D}} \:{xe}^{−{x}} {siny}\:{dy}\:{with}\:{D}\:{is}\:{the}\:{triangle} \\ $$$${OAB}\:\:\:\:{O}\left(\mathrm{0},\mathrm{0}\right)\:\:{A}\left(\mathrm{1},\mathrm{0}\right)\:{B}\left(\mathrm{0},\mathrm{1}\right) \\ $$

Question Number 89306 Answers: 0 Comments: 0

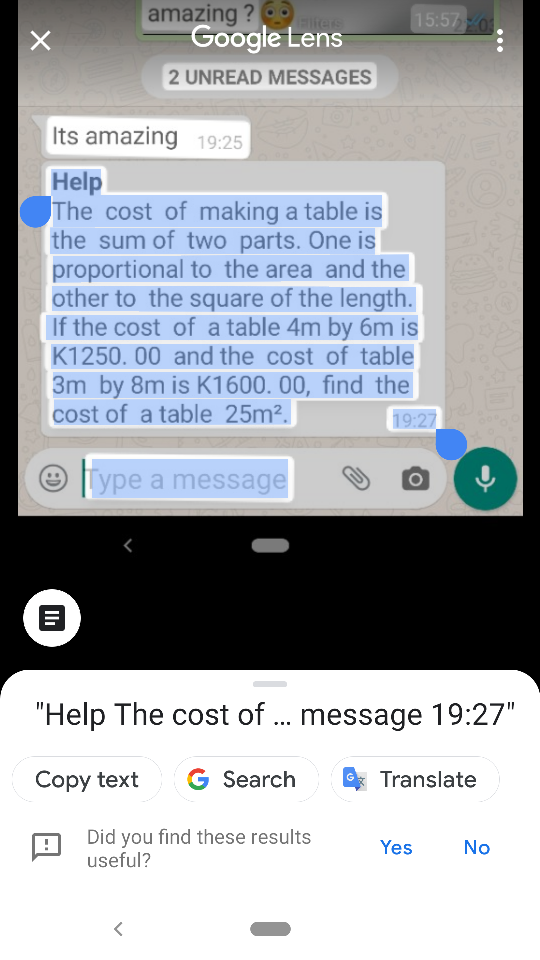
Question Number 89302 Answers: 0 Comments: 0

∫((1+cos(x)+sin(x))/x^3 )dx

$$\int\frac{\mathrm{1}+{cos}\left({x}\right)+{sin}\left({x}\right)}{{x}^{\mathrm{3}} }{dx} \\ $$

Question Number 89300 Answers: 1 Comments: 4

$$. \\ $$

Question Number 89290 Answers: 1 Comments: 2

Question Number 89362 Answers: 0 Comments: 1

∫(1/((√x)((√x)+1)^3 ))

$$\int\frac{\mathrm{1}}{\sqrt{\mathrm{x}}\left(\sqrt{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Question Number 89292 Answers: 1 Comments: 0

Question Number 89286 Answers: 2 Comments: 0

show that ∫_0 ^1 (((x^2 +1)ln(1+x))/(x^4 −x^2 +1))dx=(π/6)ln(2+(√3))

$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\pi}{\mathrm{6}}{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$

Question Number 89281 Answers: 1 Comments: 2

Question Number 89280 Answers: 0 Comments: 0

Question Number 89270 Answers: 0 Comments: 0

what is the maximum perimeter of a parallelogram ABCD which inscribed the ellipse (x^2 /4) + y^2 = 1 ?

$${what}\:{is}\:{the}\:{maximum}\: \\ $$$${perimeter}\:{of}\:{a}\:{parallelogram}\: \\ $$$${ABCD}\:{which}\:{inscribed}\:{the}\: \\ $$$${ellipse}\:\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:+\:{y}^{\mathrm{2}} \:=\:\mathrm{1}\:? \\ $$

Question Number 89268 Answers: 0 Comments: 0

Please help with this summation. Σ_(k = 0) ^n (− 1)^k ^n C_k y_(n − k) = ???

Question Number 89275 Answers: 1 Comments: 1

Question Number 89273 Answers: 1 Comments: 0

Evaluate ∫_0 ^1 (x^2 /(√(1+x^3 )))dx and given that I_(n ) =∫_0 ^1 x^n (1+x^3 )^(−(1/2)) dx show that (2n−1)I_n =2(√2)−2(n−1) for n≥3. Hence evaluate I_8 , I_7 and I_6

$${Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}{dx}\:{and}\:{given}\:{that}\:{I}_{{n}\:} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$${show}\:{that}\:\left(\mathrm{2}{n}−\mathrm{1}\right){I}_{{n}} =\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\left({n}−\mathrm{1}\right)\:{for}\:{n}\geqslant\mathrm{3}. \\ $$$${Hence}\:{evaluate}\:{I}_{\mathrm{8}} ,\:{I}_{\mathrm{7}} \:{and}\:{I}_{\mathrm{6}} \\ $$

Question Number 89271 Answers: 0 Comments: 1

(3/4)×(8/9)×((15)/(16))×...×((2499)/(2500))

$$\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{8}}{\mathrm{9}}×\frac{\mathrm{15}}{\mathrm{16}}×...×\frac{\mathrm{2499}}{\mathrm{2500}} \\ $$

Question Number 89311 Answers: 0 Comments: 0

Show that ∫_( 0) ^( 1) {∫_( 0) ^( 1) ((x−y)/((x+y)^2 ))dy}dx=∫_( 0) ^( 1) {∫_( 0) ^( 1) ((x−y)/((x+y)^2 ))dx}dy

$$\:\:{Show}\:{that} \\ $$$$\underset{\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\mathrm{1}} {\int}}\left\{\underset{\:\:\:\:\mathrm{0}} {\overset{\:\:\:\mathrm{1}} {\int}}\frac{{x}−{y}}{\left({x}+{y}\right)^{\mathrm{2}} }{dy}\right\}{dx}=\underset{\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\mathrm{1}} {\int}}\left\{\underset{\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\mathrm{1}} {\int}}\frac{{x}−{y}}{\left({x}+{y}\right)^{\mathrm{2}} }{dx}\right\}{dy} \\ $$$$ \\ $$

Question Number 89259 Answers: 0 Comments: 2

hello any good books to learn calculas and series?

$${hello}\: \\ $$$${any}\:{good}\:{books}\:{to}\:{learn}\:{calculas}\:{and} \\ $$$${series}? \\ $$

Question Number 89255 Answers: 0 Comments: 3

1⟩Σ_(k=2) ^∞ (1/(k^n k!)) 2⟩∫_0 ^∞ (xe^(1−x) −⌊x⌋e^(1−⌊x⌋) )dx

$$\mathrm{1}\rangle\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{{n}} {k}!} \\ $$$$\mathrm{2}\rangle\int_{\mathrm{0}} ^{\infty} \left({xe}^{\mathrm{1}−{x}} −\lfloor{x}\rfloor{e}^{\mathrm{1}−\lfloor{x}\rfloor} \right){dx} \\ $$

Question Number 89244 Answers: 0 Comments: 1

Question Number 89243 Answers: 3 Comments: 0

solve the following diffirntial equation 1)(2x+y)dx+(x+y)dy=0 2)(3x−y)dx−(x−y)dy=0 3) (cos(x)+y)dx + (2y+x)dy=0

$${solve}\:{the}\:{following}\:{diffirntial}\:{equation} \\ $$$$\left.\mathrm{1}\right)\left(\mathrm{2}{x}+{y}\right){dx}+\left({x}+{y}\right){dy}=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\left(\mathrm{3}{x}−{y}\right){dx}−\left({x}−{y}\right){dy}=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:\left({cos}\left({x}\right)+{y}\right){dx}\:+\:\left(\mathrm{2}{y}+{x}\right){dy}=\mathrm{0} \\ $$

Question Number 89237 Answers: 0 Comments: 1

∫_2 ^1 (x+1)((√(x+3)))

$$\int_{\mathrm{2}} ^{\mathrm{1}} \left(\mathrm{x}+\mathrm{1}\right)\left(\sqrt{\left.\mathrm{x}+\mathrm{3}\right)}\right. \\ $$

Pg 1256 Pg 1257 Pg 1258 Pg 1259 Pg 1260 Pg 1261 Pg 1262 Pg 1263 Pg 1264 Pg 1265

Contact: info@tinkutara.com