Question and Answers Forum

AllQuestion and Answers: Page 1260

Question Number 90041 Answers: 1 Comments: 0

calculste ∫_0 ^∞ ((xarctan(2x))/(9+2x^2 ))dx

$${calculste}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xarctan}\left(\mathrm{2}{x}\right)}{\mathrm{9}+\mathrm{2}{x}^{\mathrm{2}} }{dx}\: \\ $$

Question Number 90040 Answers: 0 Comments: 1

find ∫_(−∞) ^(+∞) ((ch(acosx +bsinx))/(x^2 −x+1))dx a and b reals given

$${find}\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{ch}\left({acosx}\:+{bsinx}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$${a}\:{and}\:{b}\:{reals}\:{given} \\ $$

Question Number 90038 Answers: 0 Comments: 0

Σ_(n=1) ^∞ (H_n /n^k )=S_k H_q =Σ_(p=1) ^q (1/p) Is there a simple from for S_k

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{H}_{{n}} }{{n}^{{k}} }={S}_{{k}} \:\:\:\:\:\:\:{H}_{{q}} =\underset{{p}=\mathrm{1}} {\overset{{q}} {\sum}}\frac{\mathrm{1}}{{p}} \\ $$$${Is}\:{there}\:{a}\:{simple}\:{from}\:{for}\:{S}_{{k}} \\ $$

Question Number 90030 Answers: 0 Comments: 0

Question Number 90024 Answers: 0 Comments: 2

sinh^(−1) [ln(x + (√(x^2 + 1)) )] = ?

$$\mathrm{sinh}^{−\mathrm{1}} \left[\mathrm{ln}\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:\right)\right]\:=\:? \\ $$

Question Number 90023 Answers: 1 Comments: 0

∫ e^(∣x∣) dx = ???

$$\:\int\:{e}^{\mid{x}\mid} \:{dx}\:=\:??? \\ $$

Question Number 90019 Answers: 1 Comments: 0

find the gcd(2467, 1367)

$$\mathrm{find}\:\mathrm{the}\:\mathrm{gcd}\left(\mathrm{2467},\:\mathrm{1367}\right) \\ $$

Question Number 90018 Answers: 1 Comments: 2

expand , ln(1 + sin x) right up to the term in x^3

$$\mathrm{expand}\:,\:\mathrm{ln}\left(\mathrm{1}\:+\:\mathrm{sin}\:{x}\right)\:\mathrm{right}\:\mathrm{up}\:\mathrm{to}\:\mathrm{the}\:\mathrm{term}\:\mathrm{in}\:{x}^{\mathrm{3}} \\ $$

Question Number 90013 Answers: 1 Comments: 2

−p^2 +2027=−q^2 p+q=?

$$−{p}^{\mathrm{2}} +\mathrm{2027}=−{q}^{\mathrm{2}} \\ $$$${p}+{q}=? \\ $$

Question Number 90011 Answers: 0 Comments: 6

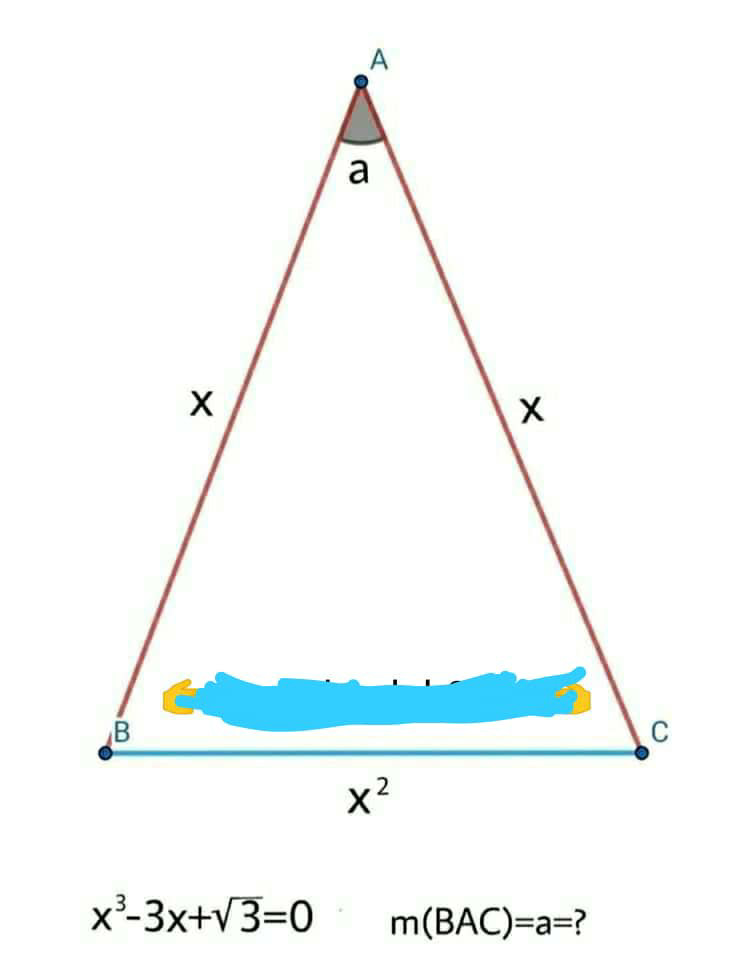
Question Number 90009 Answers: 0 Comments: 0

Σ_(n=0) ^∞ ((((√2)−1)^(2n+1) )/((2n+1)^2 ))=?

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=? \\ $$

Question Number 90003 Answers: 0 Comments: 0

show that ∫_(−∞) ^∞ (dx/(1+(x+tan(x))^(2 ) ))=π

$${show}\:{that} \\ $$$$\int_{−\infty} ^{\infty} \frac{{dx}}{\mathrm{1}+\left({x}+{tan}\left({x}\right)\right)^{\mathrm{2}\:} }=\pi \\ $$

Question Number 89994 Answers: 2 Comments: 0

x−y=3(√(xy)) ((x/y)−1)^3 +((y/x)−1)^3 = ?

$$\mathrm{x}−\mathrm{y}=\mathrm{3}\sqrt{\mathrm{xy}} \\ $$$$\left(\frac{\mathrm{x}}{\mathrm{y}}−\mathrm{1}\right)^{\mathrm{3}} +\left(\frac{\mathrm{y}}{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{3}} \:=\:? \\ $$

Question Number 89991 Answers: 0 Comments: 2

if a,b > 0 and (a^2 /b^2 ) = (5/3) find ((a^2 +b^2 )/(ab))

$$\mathrm{if}\:\mathrm{a},\mathrm{b}\:>\:\mathrm{0}\:\mathrm{and}\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{find}\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{ab}} \\ $$

Question Number 89986 Answers: 0 Comments: 3

∫_0 ^1 (−1)^(⌊(1/x)⌋) dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{\lfloor\frac{\mathrm{1}}{{x}}\rfloor} \:{dx} \\ $$

Question Number 89980 Answers: 0 Comments: 2

Question Number 89978 Answers: 0 Comments: 1

(x (dy/dx)−y)(cos (((2y)/x))) = −3x^4

$$\left(\mathrm{x}\:\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}\right)\left(\mathrm{cos}\:\left(\frac{\mathrm{2y}}{\mathrm{x}}\right)\right)\:=\:−\mathrm{3x}^{\mathrm{4}} \\ $$

Question Number 89977 Answers: 0 Comments: 2

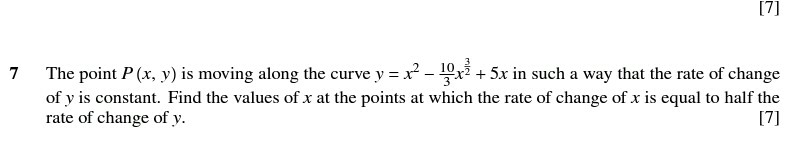
Question Number 89973 Answers: 1 Comments: 1

x (dy/dx) −y = x^2 tan ((y/x))

$${x}\:\frac{{dy}}{{dx}}\:−{y}\:=\:{x}^{\mathrm{2}} \:\mathrm{tan}\:\left(\frac{{y}}{{x}}\right)\: \\ $$

Question Number 89970 Answers: 0 Comments: 1

xy (dy/dx) = y^2 ((x^3 /(x^2 +1)))

$$\mathrm{xy}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{y}^{\mathrm{2}} \left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\: \\ $$

Question Number 89955 Answers: 1 Comments: 2

9^(x+1) ∤28(3^x )+3=0

$$\mathrm{9}^{\mathrm{x}+\mathrm{1}} \nmid\mathrm{28}\left(\mathrm{3}^{\mathrm{x}} \right)+\mathrm{3}=\mathrm{0} \\ $$

Question Number 89953 Answers: 0 Comments: 1

solvethefollowingequation 5^(2x+y) =625and2^(4x∤2y) =(1/6)

$$\mathrm{solvethefollowingequation} \\ $$$$\mathrm{5}^{\mathrm{2x}+\mathrm{y}} =\mathrm{625and2}^{\mathrm{4x}\nmid\mathrm{2y}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Question Number 89951 Answers: 0 Comments: 1

log _2 (sin (x+((5π)/(12)))) + log _2 (sin (x+(π/(12))))=−1

$$\mathrm{log}\:_{\mathrm{2}} \:\left(\mathrm{sin}\:\left({x}+\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\right)\:+\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{12}}\right)\right)=−\mathrm{1} \\ $$

Question Number 89950 Answers: 0 Comments: 1

Question Number 89946 Answers: 1 Comments: 0

∫ _(−(π/2)) ^(π/2) (dx/(1+e^(sin x) ))

$$\int\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\:}}\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} } \\ $$

Question Number 89958 Answers: 0 Comments: 1

prove that (1+sin x/1+cos 3(1sin x/1+cosec x)=tanx

$${prove}\:{that}\:\left(\mathrm{1}+\mathrm{sin}\:{x}/\mathrm{1}+\mathrm{cos}\:\mathrm{3}\left(\mathrm{1sin}\:{x}/\mathrm{1}+\mathrm{cosec}\:{x}\right)={tanx}\right. \\ $$

Pg 1255 Pg 1256 Pg 1257 Pg 1258 Pg 1259 Pg 1260 Pg 1261 Pg 1262 Pg 1263 Pg 1264

Contact: [email protected]