
AllQuestion and Answers: Page 1259
Question Number 90134 Answers: 0 Comments: 0

Question Number 90122 Answers: 0 Comments: 1
Question Number 90162 Answers: 1 Comments: 0

Question Number 90160 Answers: 1 Comments: 0
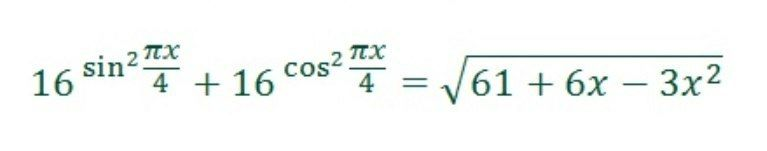
Question Number 90161 Answers: 1 Comments: 0
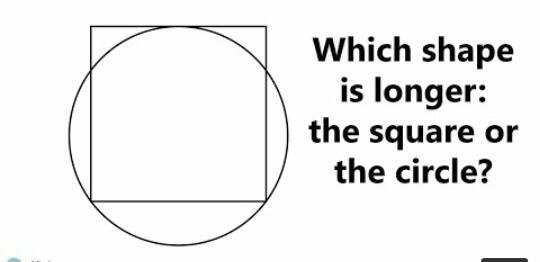
Question Number 90113 Answers: 1 Comments: 0
Question Number 90110 Answers: 0 Comments: 2
Question Number 90103 Answers: 0 Comments: 1

Question Number 90100 Answers: 1 Comments: 0
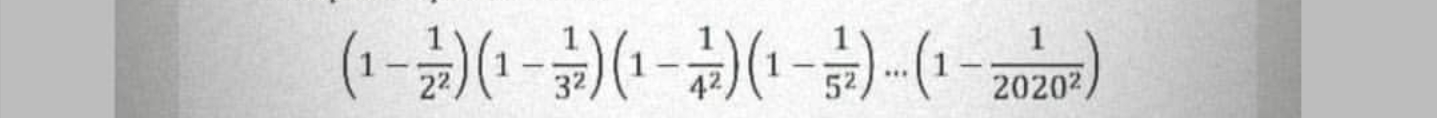
Question Number 90099 Answers: 0 Comments: 2
Question Number 90097 Answers: 0 Comments: 1
Question Number 90090 Answers: 1 Comments: 0
Question Number 90083 Answers: 0 Comments: 0

Question Number 90086 Answers: 0 Comments: 7

Question Number 90087 Answers: 0 Comments: 1
$$\underset{{k}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{{k}} }\:=\:? \\ $$
Question Number 90080 Answers: 0 Comments: 0
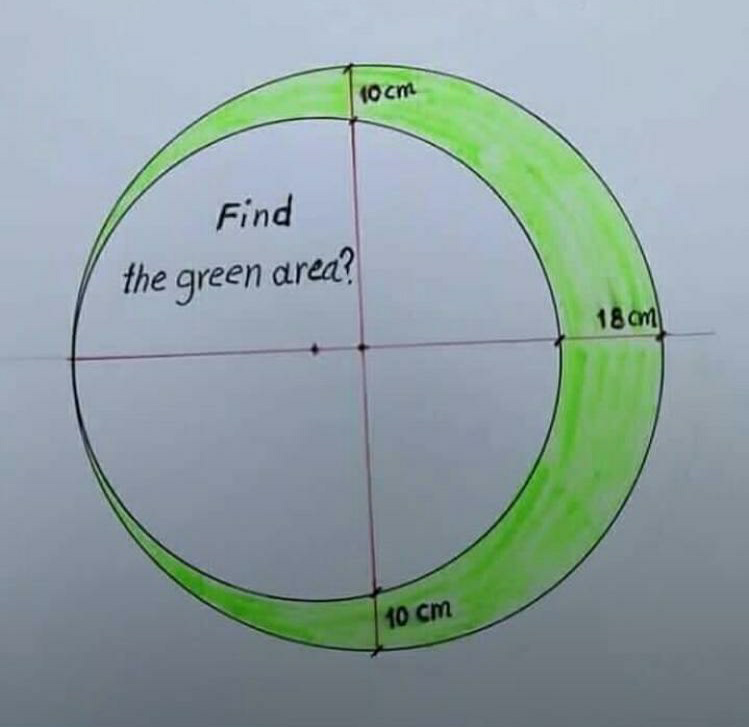
Question Number 90077 Answers: 0 Comments: 3
Question Number 90075 Answers: 0 Comments: 1
Question Number 90073 Answers: 0 Comments: 0
Question Number 90092 Answers: 0 Comments: 1
Question Number 90069 Answers: 2 Comments: 3
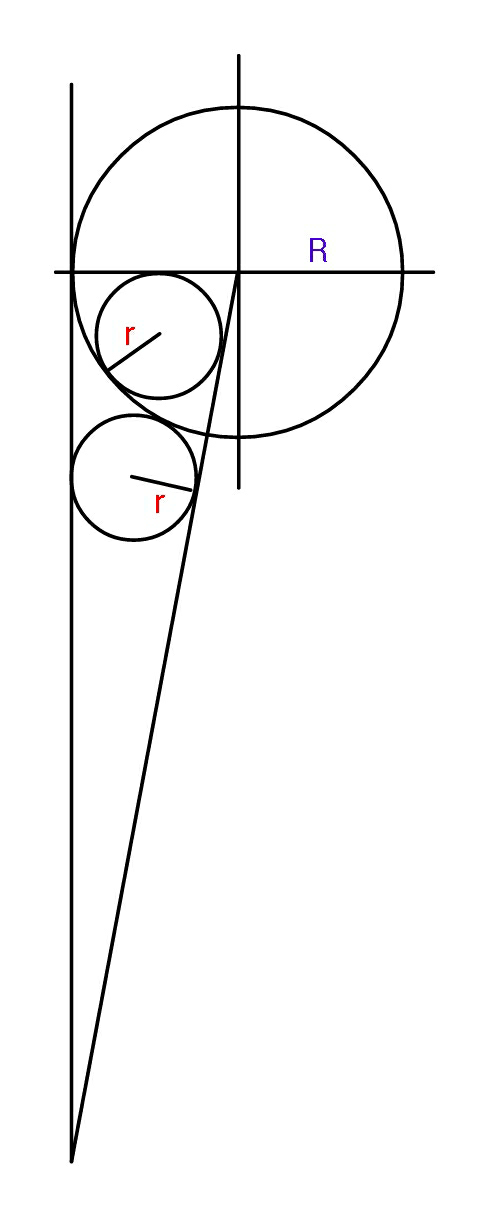
Question Number 90060 Answers: 0 Comments: 1
Question Number 90058 Answers: 1 Comments: 1
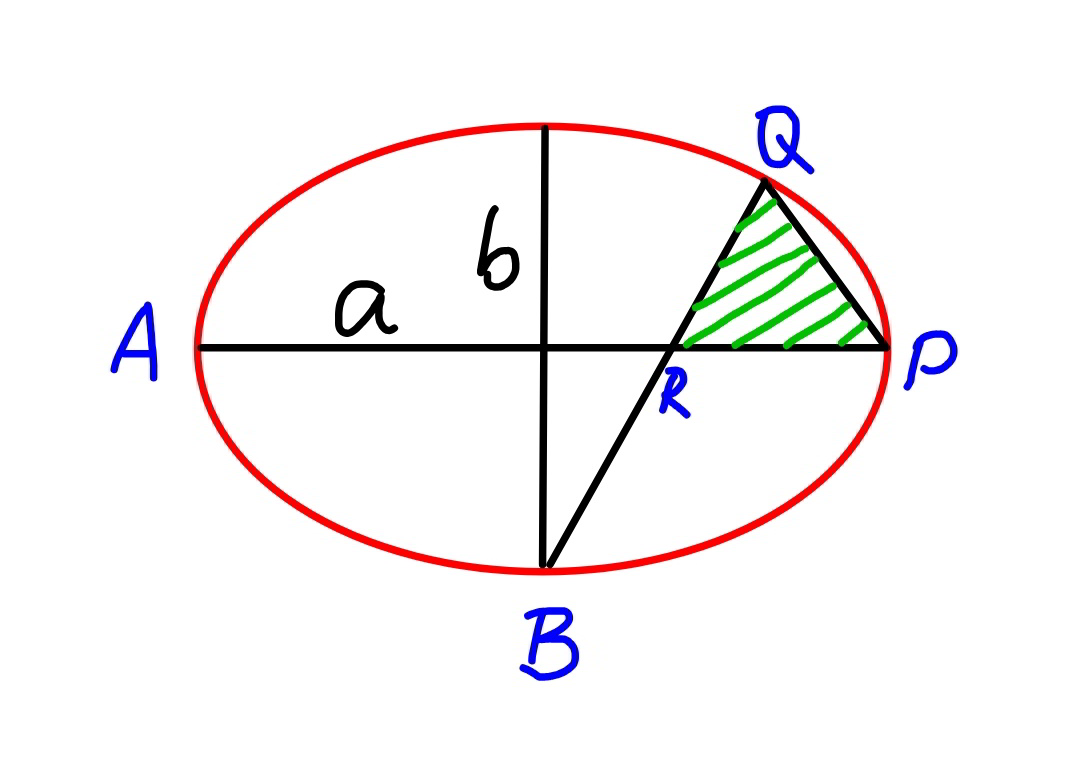
Question Number 90055 Answers: 0 Comments: 1

Question Number 90049 Answers: 0 Comments: 0

Question Number 90048 Answers: 1 Comments: 0
$$\mathrm{5}^{\sqrt{\mathrm{x}}} \:−\mathrm{5}^{\mathrm{x}−\mathrm{7}} \:=\:\mathrm{100} \\ $$
Pg 1254 Pg 1255 Pg 1256 Pg 1257 Pg 1258 Pg 1259 Pg 1260 Pg 1261 Pg 1262 Pg 1263
