
AllQuestion and Answers: Page 1241
Question Number 92182 Answers: 0 Comments: 4

Question Number 92179 Answers: 0 Comments: 12
Question Number 92170 Answers: 0 Comments: 3
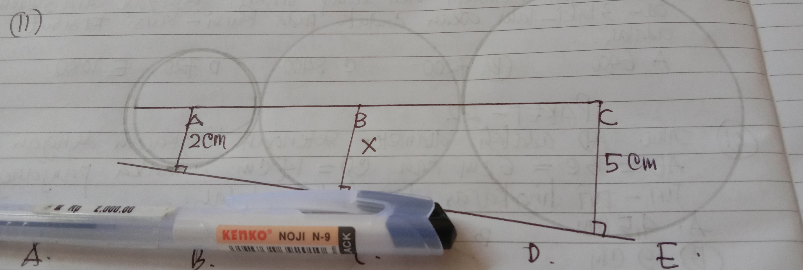
Question Number 92167 Answers: 1 Comments: 1
Question Number 92193 Answers: 0 Comments: 2
Question Number 92156 Answers: 0 Comments: 1
Question Number 92151 Answers: 0 Comments: 1
Question Number 92146 Answers: 1 Comments: 1
Question Number 92143 Answers: 0 Comments: 1
$${fond}\int\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$
Question Number 92138 Answers: 2 Comments: 0
Question Number 92137 Answers: 0 Comments: 2
Question Number 92135 Answers: 0 Comments: 5
$${a}^{{x}} \:=\:\mathrm{log}\:_{{a}} \:\left({x}\right) \\ $$$${a}=? \\ $$
Question Number 92134 Answers: 0 Comments: 1
Question Number 92133 Answers: 0 Comments: 0
Question Number 92126 Answers: 0 Comments: 0
$$\int\:\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}{{x}+\mathrm{1}}}\:{dx}\: \\ $$
Question Number 92120 Answers: 0 Comments: 0
$$\int_{−\mathrm{3}} ^{\mathrm{4}} \lfloor{x}.\lceil{x}^{\mathrm{2}} \rceil\rfloor\:{dx} \\ $$
Question Number 92119 Answers: 0 Comments: 3
Question Number 92118 Answers: 1 Comments: 3
Question Number 92117 Answers: 0 Comments: 3
Question Number 92116 Answers: 0 Comments: 0
Question Number 92115 Answers: 1 Comments: 0
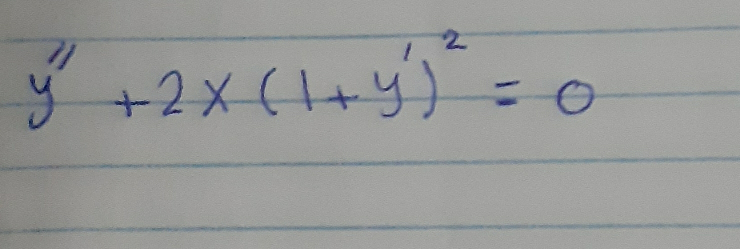
Question Number 92114 Answers: 1 Comments: 0
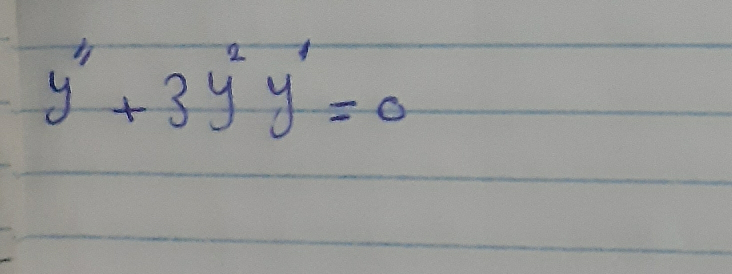
Question Number 92102 Answers: 2 Comments: 3
$${how}\:{can}\:{we}\:{factorize}\:\:\:{x}^{\mathrm{5}} −\mathrm{1}\:\:? \\ $$
Question Number 92089 Answers: 0 Comments: 0
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}+{sinx}\right){dx} \\ $$
Question Number 92088 Answers: 0 Comments: 0
Question Number 92087 Answers: 0 Comments: 1
Pg 1236 Pg 1237 Pg 1238 Pg 1239 Pg 1240 Pg 1241 Pg 1242 Pg 1243 Pg 1244 Pg 1245
