
AllQuestion and Answers: Page 1237
Question Number 92723 Answers: 1 Comments: 0

Question Number 92717 Answers: 2 Comments: 5

Question Number 92708 Answers: 1 Comments: 0
Question Number 92702 Answers: 2 Comments: 0
$${y}''+\mathrm{2}{y}'−\mathrm{3}{y}={e}^{{x}} +{e}^{\mathrm{2}{x}} \\ $$
Question Number 92701 Answers: 0 Comments: 3

Question Number 92700 Answers: 0 Comments: 0
Question Number 92691 Answers: 1 Comments: 3
Question Number 92687 Answers: 0 Comments: 0
Question Number 92684 Answers: 1 Comments: 4

Question Number 92682 Answers: 0 Comments: 5
Question Number 92712 Answers: 0 Comments: 2
Question Number 92673 Answers: 1 Comments: 2
Question Number 92668 Answers: 1 Comments: 2
Question Number 92646 Answers: 0 Comments: 22

Question Number 92626 Answers: 0 Comments: 1
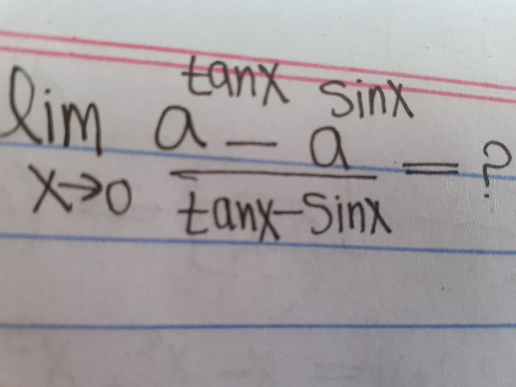
Question Number 92624 Answers: 0 Comments: 0

Question Number 92621 Answers: 0 Comments: 1

Question Number 92619 Answers: 0 Comments: 0
Question Number 92608 Answers: 0 Comments: 4

Question Number 92605 Answers: 1 Comments: 4
Question Number 92635 Answers: 0 Comments: 9

Question Number 92597 Answers: 0 Comments: 1
Question Number 92594 Answers: 0 Comments: 5

Question Number 92593 Answers: 0 Comments: 0
Question Number 92585 Answers: 0 Comments: 1
Question Number 92577 Answers: 1 Comments: 3
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{x}} \\ $$
Pg 1232 Pg 1233 Pg 1234 Pg 1235 Pg 1236 Pg 1237 Pg 1238 Pg 1239 Pg 1240 Pg 1241
