
AllQuestion and Answers: Page 1235
Question Number 92425 Answers: 0 Comments: 1
Question Number 92424 Answers: 0 Comments: 3
Question Number 92423 Answers: 1 Comments: 0
Question Number 92422 Answers: 0 Comments: 0
Question Number 92421 Answers: 1 Comments: 0
Question Number 92420 Answers: 2 Comments: 2

Question Number 92447 Answers: 0 Comments: 1
Question Number 92410 Answers: 0 Comments: 3
Question Number 92407 Answers: 0 Comments: 0
Question Number 92399 Answers: 0 Comments: 1
Question Number 92398 Answers: 1 Comments: 0
Question Number 92397 Answers: 0 Comments: 2
Question Number 92394 Answers: 0 Comments: 2
$$\int\:\mathrm{ln}\:\left(\sqrt{\mathrm{1}−{x}}\:+\:\sqrt{\mathrm{1}+{x}}\:\right)\:{dx}\: \\ $$
Question Number 92390 Answers: 0 Comments: 2
Question Number 92366 Answers: 0 Comments: 3

Question Number 92356 Answers: 0 Comments: 7

Question Number 92379 Answers: 1 Comments: 5
Question Number 92347 Answers: 1 Comments: 3

Question Number 92346 Answers: 3 Comments: 3
Question Number 92344 Answers: 0 Comments: 3
Question Number 92340 Answers: 0 Comments: 2
Question Number 92337 Answers: 0 Comments: 0

Question Number 92335 Answers: 0 Comments: 0
$$\sqrt{\left\{\mathrm{x}\right\}}\:=\:\mathrm{1}+\:\mathrm{ln}\left(\mathrm{x}\right)\: \\ $$
Question Number 92334 Answers: 0 Comments: 0
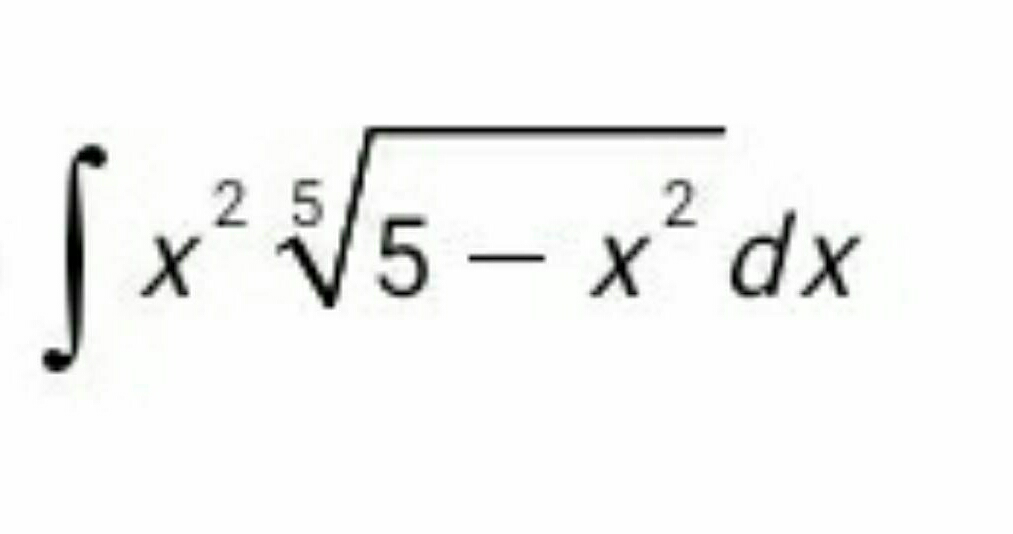
Question Number 92324 Answers: 1 Comments: 0
Question Number 92323 Answers: 2 Comments: 3

Pg 1230 Pg 1231 Pg 1232 Pg 1233 Pg 1234 Pg 1235 Pg 1236 Pg 1237 Pg 1238 Pg 1239
