
AllQuestion and Answers: Page 1232
Question Number 93376 Answers: 0 Comments: 1
Question Number 93371 Answers: 0 Comments: 21
Question Number 93368 Answers: 1 Comments: 0
Question Number 93367 Answers: 0 Comments: 2
Question Number 93366 Answers: 1 Comments: 0
Question Number 93365 Answers: 0 Comments: 3
Question Number 93350 Answers: 1 Comments: 0
Question Number 93340 Answers: 1 Comments: 7
Question Number 93331 Answers: 1 Comments: 2
Question Number 93330 Answers: 1 Comments: 0
Question Number 93315 Answers: 0 Comments: 0
Question Number 93312 Answers: 1 Comments: 0
Question Number 93304 Answers: 5 Comments: 5
$$\int\sqrt{\mathrm{tan}\:\left({x}\right)}{dx}\:{Who}\:{can}\:{solve}\:{this}\:{problem}? \\ $$
Question Number 93299 Answers: 0 Comments: 2
Question Number 93296 Answers: 1 Comments: 1
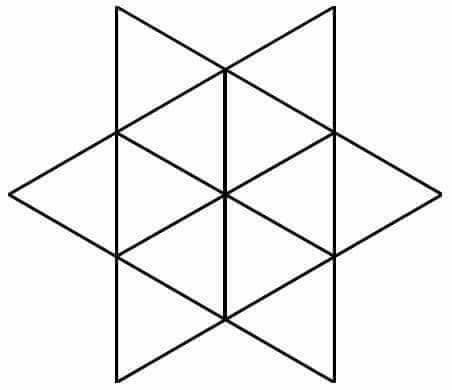
Question Number 93287 Answers: 0 Comments: 1

Question Number 93265 Answers: 1 Comments: 1
Question Number 93258 Answers: 1 Comments: 1

Question Number 93256 Answers: 0 Comments: 2
Question Number 93283 Answers: 0 Comments: 0
Question Number 93284 Answers: 0 Comments: 5

Question Number 93249 Answers: 0 Comments: 4
Question Number 93248 Answers: 1 Comments: 1
Question Number 93241 Answers: 1 Comments: 0
Question Number 93239 Answers: 2 Comments: 3
Question Number 93227 Answers: 0 Comments: 4

Pg 1227 Pg 1228 Pg 1229 Pg 1230 Pg 1231 Pg 1232 Pg 1233 Pg 1234 Pg 1235 Pg 1236
