
AllQuestion and Answers: Page 1231
Question Number 93483 Answers: 0 Comments: 0
Question Number 93481 Answers: 1 Comments: 1
$$\int\left(\mathrm{log}\:\mathrm{x}/\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}= \\ $$
Question Number 93478 Answers: 0 Comments: 2
Question Number 93477 Answers: 2 Comments: 0
Question Number 93474 Answers: 2 Comments: 0
Question Number 93473 Answers: 1 Comments: 1
$$\int\mathrm{1}/\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$
Question Number 93471 Answers: 1 Comments: 0
Question Number 93470 Answers: 1 Comments: 4
Question Number 93467 Answers: 1 Comments: 0
Question Number 93464 Answers: 1 Comments: 0
Question Number 93460 Answers: 1 Comments: 1
Question Number 93451 Answers: 0 Comments: 3
Question Number 93450 Answers: 2 Comments: 0
Question Number 93442 Answers: 0 Comments: 3
Question Number 93446 Answers: 0 Comments: 1
Question Number 93439 Answers: 2 Comments: 0
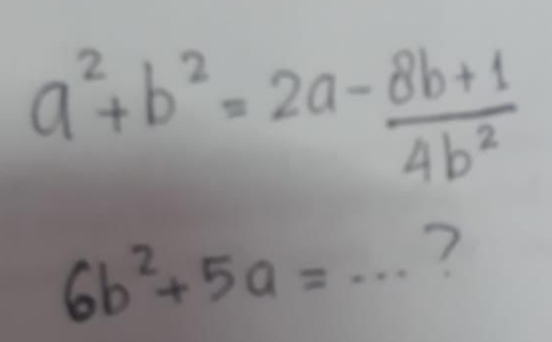
Question Number 93434 Answers: 1 Comments: 1

Question Number 93428 Answers: 1 Comments: 0

Question Number 93418 Answers: 0 Comments: 3
Question Number 93415 Answers: 0 Comments: 5
Question Number 93414 Answers: 0 Comments: 0
Question Number 93410 Answers: 0 Comments: 7
$$\int\frac{\mathrm{1}+{x}^{\mathrm{6}} }{\mathrm{1}+{x}^{\mathrm{8}} }{dx} \\ $$
Question Number 93397 Answers: 0 Comments: 2
Question Number 93388 Answers: 0 Comments: 2

Question Number 93376 Answers: 0 Comments: 1
Question Number 93371 Answers: 0 Comments: 21
Pg 1226 Pg 1227 Pg 1228 Pg 1229 Pg 1230 Pg 1231 Pg 1232 Pg 1233 Pg 1234 Pg 1235
