
AllQuestion and Answers: Page 1230
Question Number 93638 Answers: 2 Comments: 2
Question Number 93623 Answers: 0 Comments: 2

Question Number 93620 Answers: 1 Comments: 0
Question Number 93618 Answers: 0 Comments: 1
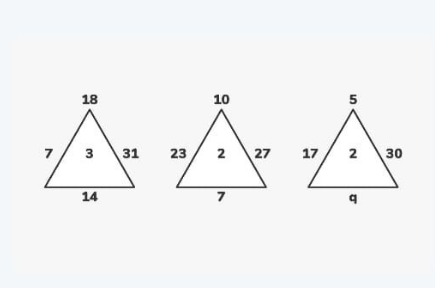
Question Number 93610 Answers: 1 Comments: 0
$$\int\left(\frac{\sqrt{\mathrm{x}^{\mathrm{n}} +\mathrm{1}}}{\mathrm{x}}\right)\mathrm{dx} \\ $$
Question Number 93587 Answers: 3 Comments: 0
Question Number 93705 Answers: 0 Comments: 3
Question Number 93571 Answers: 0 Comments: 1
Question Number 93569 Answers: 0 Comments: 0
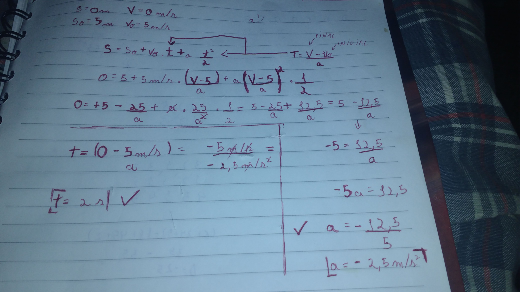
Question Number 93568 Answers: 0 Comments: 1

Question Number 93567 Answers: 1 Comments: 1
Question Number 93555 Answers: 0 Comments: 3
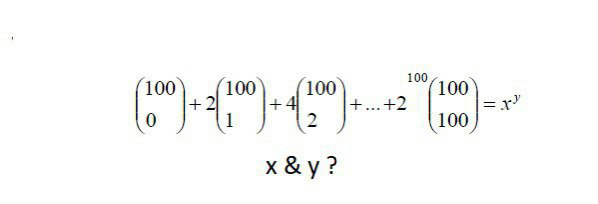
Question Number 93553 Answers: 0 Comments: 2
$$\int{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{u}} \right)\mathrm{du} \\ $$
Question Number 93546 Answers: 0 Comments: 13
Question Number 93540 Answers: 0 Comments: 7

Question Number 93720 Answers: 0 Comments: 2
Question Number 93534 Answers: 1 Comments: 0
Question Number 93530 Answers: 0 Comments: 4
Question Number 93513 Answers: 1 Comments: 0
Question Number 93509 Answers: 0 Comments: 5
Question Number 93505 Answers: 0 Comments: 0
Question Number 93512 Answers: 0 Comments: 2
Question Number 93510 Answers: 0 Comments: 1
$${y}^{'} −{y}.\mathrm{tan}\:{x}+{y}^{\mathrm{2}} \mathrm{cos}\:{x}=\mathrm{0} \\ $$
Question Number 93493 Answers: 0 Comments: 4
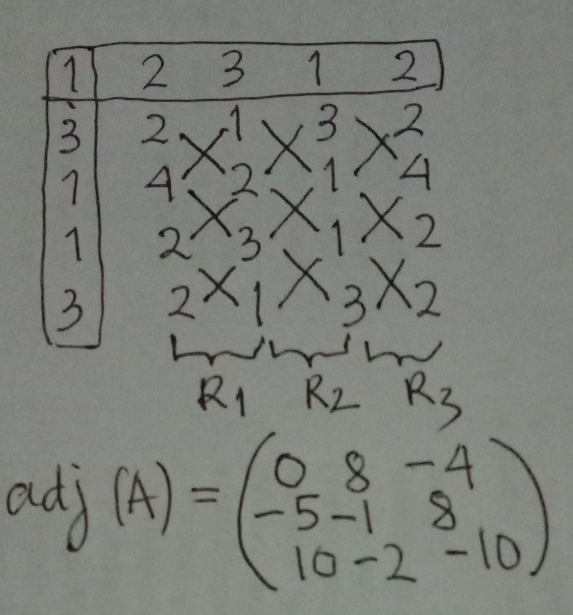
Question Number 93484 Answers: 0 Comments: 2
Question Number 93483 Answers: 0 Comments: 0
Pg 1225 Pg 1226 Pg 1227 Pg 1228 Pg 1229 Pg 1230 Pg 1231 Pg 1232 Pg 1233 Pg 1234
