
AllQuestion and Answers: Page 1227
Question Number 94119 Answers: 0 Comments: 1
$$\int\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\: \\ $$
Question Number 94096 Answers: 1 Comments: 1
Question Number 94095 Answers: 0 Comments: 0
Question Number 94093 Answers: 0 Comments: 0
Question Number 94117 Answers: 0 Comments: 8
Question Number 93991 Answers: 1 Comments: 11

Question Number 93982 Answers: 0 Comments: 7
$$\mathrm{LCM}\left({a},\frac{\mathrm{3}}{\mathrm{5}}{a}\right)=\mathrm{3}{a}\: \\ $$$${a}=? \\ $$
Question Number 93976 Answers: 1 Comments: 10
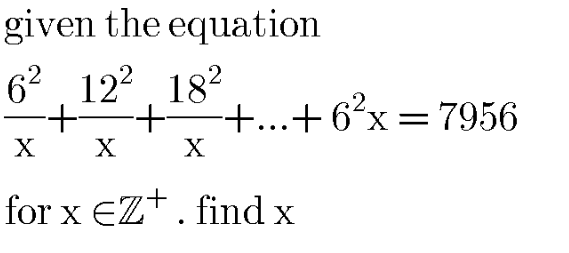
Question Number 93986 Answers: 2 Comments: 0

Question Number 93963 Answers: 0 Comments: 12
Question Number 93959 Answers: 1 Comments: 0
$$\int\left(\mathrm{tan3x}+\mathrm{sec3x}\right)\mathrm{dx}= \\ $$
Question Number 93958 Answers: 2 Comments: 1
$$\int\frac{\mathrm{sinx}−\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}= \\ $$
Question Number 93957 Answers: 0 Comments: 9
Question Number 93955 Answers: 1 Comments: 0
Question Number 93953 Answers: 2 Comments: 0

Question Number 93952 Answers: 1 Comments: 0
Question Number 93950 Answers: 2 Comments: 0
Question Number 93941 Answers: 0 Comments: 2
Question Number 93940 Answers: 0 Comments: 2
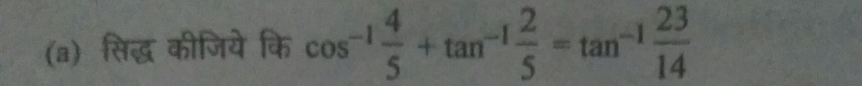
Question Number 93937 Answers: 0 Comments: 5
$$\int\frac{\mathrm{1}}{\sqrt{\mathrm{tan}\:{x}}}{dx}=? \\ $$
Question Number 93933 Answers: 0 Comments: 5
Question Number 93916 Answers: 0 Comments: 2

Question Number 93911 Answers: 0 Comments: 8
Question Number 93908 Answers: 0 Comments: 2
Question Number 93907 Answers: 2 Comments: 4
Question Number 93906 Answers: 0 Comments: 0
Pg 1222 Pg 1223 Pg 1224 Pg 1225 Pg 1226 Pg 1227 Pg 1228 Pg 1229 Pg 1230 Pg 1231
