
AllQuestion and Answers: Page 1226
Question Number 94161 Answers: 1 Comments: 2
$$\int\:\frac{\mathrm{dx}}{\mathrm{p}+\sqrt{\mathrm{qx}+\mathrm{r}}}\: \\ $$
Question Number 94158 Answers: 0 Comments: 3

Question Number 94148 Answers: 0 Comments: 0
Question Number 94144 Answers: 0 Comments: 2
Question Number 94143 Answers: 1 Comments: 3
$$\int\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:= \\ $$
Question Number 94135 Answers: 0 Comments: 2
Question Number 94134 Answers: 0 Comments: 1
Question Number 94108 Answers: 0 Comments: 0

Question Number 94084 Answers: 0 Comments: 2
Question Number 94081 Answers: 0 Comments: 0
Question Number 94080 Answers: 1 Comments: 0
Question Number 94079 Answers: 3 Comments: 0
Question Number 94078 Answers: 0 Comments: 0
Question Number 94071 Answers: 1 Comments: 2

Question Number 94125 Answers: 1 Comments: 0
Question Number 94124 Answers: 0 Comments: 3
$$\mathrm{20}+{a}={a}\:{cosh}\left(\frac{\mathrm{75}}{{a}}\right) \\ $$$${a}=? \\ $$
Question Number 94123 Answers: 0 Comments: 0
Question Number 94114 Answers: 0 Comments: 1
Question Number 94110 Answers: 1 Comments: 2
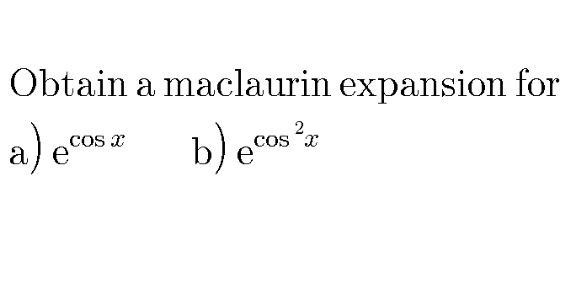
Question Number 94025 Answers: 0 Comments: 5
Question Number 94020 Answers: 0 Comments: 4

Question Number 94383 Answers: 4 Comments: 0
Question Number 94098 Answers: 1 Comments: 1
Question Number 94097 Answers: 2 Comments: 1
Question Number 94119 Answers: 0 Comments: 1
$$\int\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\: \\ $$
Question Number 94096 Answers: 1 Comments: 1
Pg 1221 Pg 1222 Pg 1223 Pg 1224 Pg 1225 Pg 1226 Pg 1227 Pg 1228 Pg 1229 Pg 1230
