
AllQuestion and Answers: Page 1225
Question Number 94297 Answers: 0 Comments: 1

Question Number 94296 Answers: 0 Comments: 0
Question Number 94291 Answers: 1 Comments: 2

Question Number 94286 Answers: 0 Comments: 0

Question Number 94285 Answers: 1 Comments: 3
Question Number 94278 Answers: 0 Comments: 5
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{\sqrt{{x}}} }{\sqrt{{x}}}{dx} \\ $$
Question Number 94273 Answers: 0 Comments: 1

Question Number 94269 Answers: 0 Comments: 2

Question Number 94257 Answers: 2 Comments: 0
Question Number 94245 Answers: 1 Comments: 0
Question Number 94241 Answers: 1 Comments: 1
Question Number 94239 Answers: 1 Comments: 0
Question Number 94237 Answers: 1 Comments: 1

Question Number 94243 Answers: 0 Comments: 3
Question Number 94220 Answers: 0 Comments: 5
Question Number 94219 Answers: 1 Comments: 1
$$\int\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \mathrm{dx}=? \\ $$
Question Number 94214 Answers: 0 Comments: 4
Question Number 94212 Answers: 1 Comments: 0
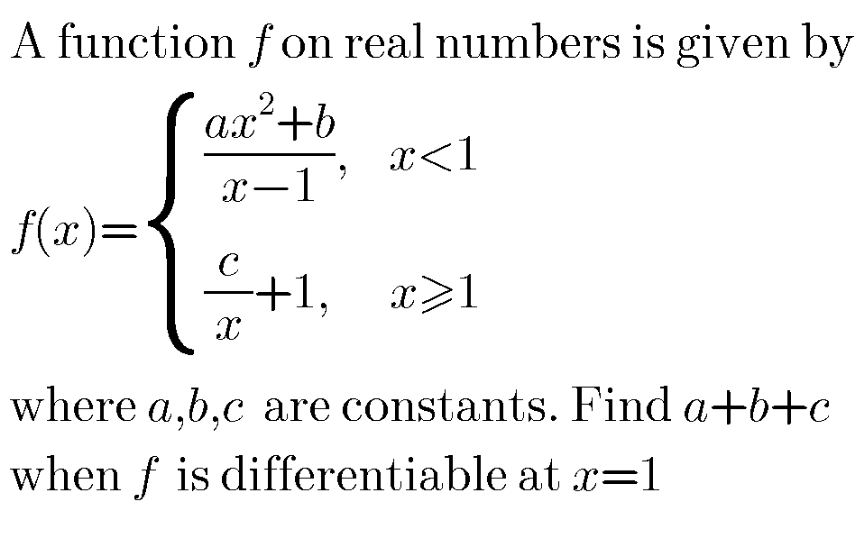
Question Number 94201 Answers: 1 Comments: 1

Question Number 94210 Answers: 1 Comments: 0
$$\frac{{s}\left({t}+\Delta{t}\right)−{s}\left({t}\right)}{\Delta{t}} \\ $$
Question Number 94193 Answers: 0 Comments: 5

Question Number 94191 Answers: 1 Comments: 0

Question Number 94186 Answers: 0 Comments: 1
Question Number 94184 Answers: 4 Comments: 1
Question Number 94174 Answers: 1 Comments: 3
Question Number 94161 Answers: 1 Comments: 2
$$\int\:\frac{\mathrm{dx}}{\mathrm{p}+\sqrt{\mathrm{qx}+\mathrm{r}}}\: \\ $$
Pg 1220 Pg 1221 Pg 1222 Pg 1223 Pg 1224 Pg 1225 Pg 1226 Pg 1227 Pg 1228 Pg 1229
