Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1224

Question Number 86946 Answers: 0 Comments: 2

Question Number 86937 Answers: 0 Comments: 4

Question Number 86932 Answers: 1 Comments: 0

Question Number 86924 Answers: 1 Comments: 0

Question Number 86918 Answers: 0 Comments: 2

Question Number 86915 Answers: 0 Comments: 0

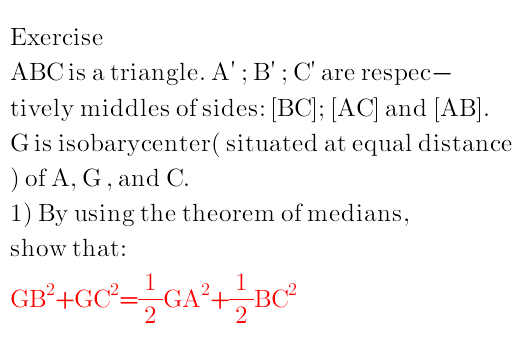
Question Number 86914 Answers: 0 Comments: 0

Question Number 86907 Answers: 1 Comments: 2

Question Number 86903 Answers: 0 Comments: 0

Question Number 86902 Answers: 0 Comments: 2

Mr.mathmax by abdo i request you to check my process to your question 86375.

$${Mr}.{mathmax}\:{by}\:{abdo} \\ $$$${i}\:{request}\:{you}\:{to}\:{check} \\ $$$${my}\:{process}\:{to}\:{your} \\ $$$${question}\:\mathrm{86375}. \\ $$

Question Number 86897 Answers: 1 Comments: 1

If ∫ (1/((x^2 +1)(x^2 +4))) dx = A tan^(−1) x+B tan^(−1) (x/2)+C, then

$$\mathrm{If}\:\int\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:=\:\:{A}\:\mathrm{tan}^{−\mathrm{1}} {x}+{B}\:\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\mathrm{2}}+{C},\:\mathrm{then} \\ $$

Question Number 86895 Answers: 0 Comments: 0

A small mass rest on a horizontal plat form which vibrates vertically in simple harmonic motion with period 0.50s. Find the maximum amplitude of the motion which allow which allow the mass to remain in contact with the platform throughout the motion

$$\mathrm{A}\:\mathrm{small}\:\mathrm{mass}\:\mathrm{rest}\:\mathrm{on}\:\mathrm{a}\:\mathrm{horizontal}\:\mathrm{plat}\:\mathrm{form}\:\mathrm{which}\:\mathrm{vibrates}\: \\ $$$$\mathrm{vertically}\:\mathrm{in}\:\mathrm{simple}\:\mathrm{harmonic}\:\mathrm{motion}\:\mathrm{with}\:\mathrm{period}\:\mathrm{0}.\mathrm{50s}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{amplitude}\:\mathrm{of}\:\mathrm{the}\:\mathrm{motion}\:\mathrm{which}\:\mathrm{allow}\:\mathrm{which} \\ $$$$\mathrm{allow}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{to}\:\mathrm{remain}\:\mathrm{in}\:\mathrm{contact}\:\mathrm{with}\:\mathrm{the}\:\mathrm{platform}\:\mathrm{throughout} \\ $$$$\mathrm{the}\:\mathrm{motion} \\ $$

Question Number 86894 Answers: 0 Comments: 2

let f(x)=((1−x^2 )/(⌈x−1⌉)) find the domain and f ′(−(1/2)) if exist. ⌈...⌉ ceiling function

$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\lceil{x}−\mathrm{1}\rceil} \\ $$$${find}\:{the}\:{domain}\:{and}\:{f}\:'\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\:{if}\:{exist}. \\ $$$$ \\ $$$$\lceil...\rceil\:{ceiling}\:{function} \\ $$

Question Number 86886 Answers: 0 Comments: 1

Question Number 86878 Answers: 2 Comments: 1

If sin^(10) (x) + cos^(10) (x) = ((11)/(36)) find sin^(12) (x) + cos ^(12) (x) = ?

$$\mathrm{If}\:\mathrm{sin}\:^{\mathrm{10}} \:\left(\mathrm{x}\right)\:+\:\mathrm{cos}\:^{\mathrm{10}} \:\left(\mathrm{x}\right)\:=\:\frac{\mathrm{11}}{\mathrm{36}} \\ $$$$\mathrm{find}\:\mathrm{sin}\:^{\mathrm{12}} \:\left(\mathrm{x}\right)\:+\:\mathrm{cos}\:\:^{\mathrm{12}} \left(\mathrm{x}\right)\:=\:? \\ $$

Question Number 86874 Answers: 0 Comments: 0

A businessman bought 300 company shares at K60.00. The nominal price was K30.00. How much does he pay for the shares?

$${A}\:{businessman}\:{bought}\:\mathrm{300}\:{company}\:{shares}\:{at}\:\boldsymbol{\mathrm{K}}\mathrm{60}.\mathrm{00}.\:{The}\:{nominal}\:{price}\:{was}\:\boldsymbol{\mathrm{K}}\mathrm{30}.\mathrm{00}.\:{How}\:{much}\:{does}\:{he}\:{pay}\:{for}\:{the}\:{shares}? \\ $$

Question Number 86873 Answers: 0 Comments: 0

A company paid a total dividend of K12 600.00 at the end of 2018 on 6000 shares. If Freddy owned 200 shares in the company, how much was paid out in dividents to him?

$${A}\:{company}\:{paid}\:{a}\:{total}\:{dividend}\:{of}\:\boldsymbol{\mathrm{K}}\mathrm{12}\:\mathrm{600}.\mathrm{00}\:{at}\:{the}\:{end}\:{of}\:\mathrm{2018}\:{on}\:\mathrm{6000}\:{shares}.\:{If}\:{Freddy}\:{owned}\:\mathrm{200}\:{shares}\:{in}\:{the}\:{company},\:{how}\:{much}\:{was}\:{paid}\:{out}\:{in}\:{dividents}\:{to}\:{him}? \\ $$

Question Number 86871 Answers: 2 Comments: 1

∫ (dx/((x^4 +1)^3 ))

$$\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Question Number 87017 Answers: 1 Comments: 0

$$ \\ $$

Question Number 86855 Answers: 1 Comments: 0

If a,b ,c are the roots of the equation x^3 +6x^2 −4x+3 = 0 . find the equation with roots a+b , b+c , a+c ?

$$\mathrm{If}\:\mathrm{a},\mathrm{b}\:,\mathrm{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\:=\:\mathrm{0}\:.\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{equation}\:\mathrm{with}\:\mathrm{roots}\:\mathrm{a}+\mathrm{b}\:,\:\mathrm{b}+\mathrm{c}\:,\:\mathrm{a}+\mathrm{c}\:? \\ $$

Question Number 86853 Answers: 1 Comments: 0

∫((x^6 −x^3 +2)/(x^4 −x^2 −2))dx

$$\int\frac{{x}^{\mathrm{6}} −{x}^{\mathrm{3}} +\mathrm{2}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{2}}{dx} \\ $$