
AllQuestion and Answers: Page 1223
Question Number 94522 Answers: 3 Comments: 0
Question Number 94521 Answers: 3 Comments: 3
Question Number 94520 Answers: 4 Comments: 0
$$\int\:\sqrt{{e}^{\mathrm{4}{x}} +\mathrm{1}}\:{dx}\: \\ $$
Question Number 94510 Answers: 0 Comments: 3
$$\int\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{sin}\:{x}.\mathrm{cos}\:{x}}{dx}\: \\ $$
Question Number 94508 Answers: 2 Comments: 0

Question Number 94500 Answers: 1 Comments: 0
Question Number 94479 Answers: 1 Comments: 0
Question Number 94463 Answers: 0 Comments: 2
Question Number 94457 Answers: 1 Comments: 0
Question Number 94456 Answers: 1 Comments: 0
Question Number 94455 Answers: 1 Comments: 3
Question Number 94448 Answers: 3 Comments: 2
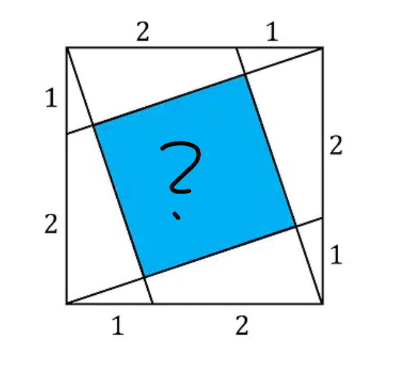
Question Number 94434 Answers: 0 Comments: 0
$${what}\:{is}\:{super}-{erf}\left({y}\right)−{hyper}\:? \\ $$
Question Number 94432 Answers: 0 Comments: 3
Question Number 95190 Answers: 1 Comments: 1

Question Number 94424 Answers: 1 Comments: 4
$$\mathrm{y}=\mathrm{x}^{\mathrm{x}} \\ $$$$\mathrm{y}^{'} =? \\ $$
Question Number 94419 Answers: 0 Comments: 0
Question Number 94418 Answers: 3 Comments: 0
Question Number 94416 Answers: 0 Comments: 0
Question Number 94397 Answers: 1 Comments: 0
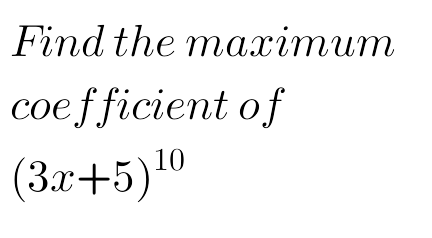
Question Number 94406 Answers: 0 Comments: 5

Question Number 94382 Answers: 1 Comments: 2
Question Number 94374 Answers: 0 Comments: 2
Question Number 94366 Answers: 1 Comments: 9
Question Number 94360 Answers: 1 Comments: 3

Question Number 94359 Answers: 0 Comments: 1
Pg 1218 Pg 1219 Pg 1220 Pg 1221 Pg 1222 Pg 1223 Pg 1224 Pg 1225 Pg 1226 Pg 1227
